
・波の干渉問題の解き方がわからない
・干渉問題が苦手
今回は、そんな悩みを持つ人向けに、例題を通して波の干渉問題の解き方について紹介していきます。
僕も、高校生の時は波の干渉問題は苦手でしたが、解き方を覚えてからは楽に解けるようになりました。
この記事を読めば、例題を通して干渉問題の解き方が勉強できるので、苦手な人は見ていってください。
※【波の干渉条件は公式を覚えるな!原理を理解して暗記量を減らす方法をわかりやすく解説】の記事をまだ読んでいない人は、先に読むことをおススメします。
✔この記事の内容
・同位相波源の干渉問題
・壁がある干渉問題の解き方
✔この記事の信頼性
苦手だった物理を、浪人時に偏差値65以上センター試験満点近くまで伸ばした、参考書には書かれていない、考え方や勉強法について、必要なエッセンスを『ぎゅっと』凝縮してまとめています。
【例題1】波の干渉問題
例題
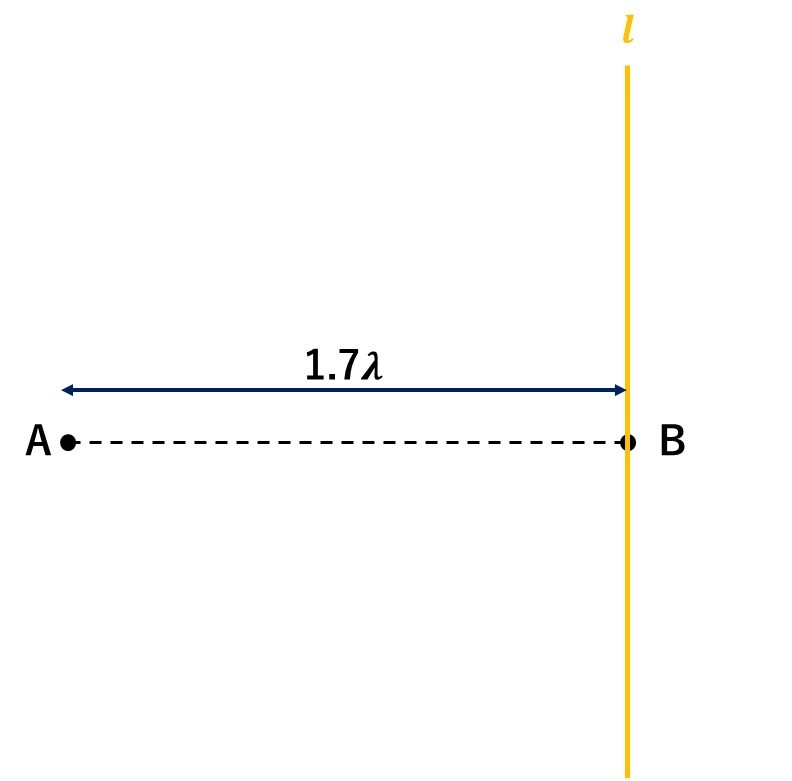
同位相波源を出す点A,Bがある。以下の直線と弱め合う線(節線)との交わる点の個数を求めよ。
(1)AB上(2)直線\(l\)上
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは、解説していくよ!

解法①:波の干渉問題
先に解き方を説明しておくと、以下のようになります!
ココがポイント
➁同位相波源であれば、2点の中点は腹になるので、半波長の腹と一致するように図を描く!
➂➀で求めた数の波長を描き込み、双曲線を描く
まず考えることは、同位相波源において、波源2点から等距離の部分は強め合いの線(腹線)になるので、それを図に描き込みましょう。
2点の中心は、経路差が0なので、強め合う(0・\(\lambda\))ので、腹になるのでした!


半波長は、波のウェーブ1個分の半分のことなので、その長さは波長\(\lambda\)の半分になります。
半波長の真ん中の『山、谷』のところが、強め合いの点で、節の部分が弱め合いの点です。
※さらっと書いていますが、半波長の理解は非常に大切です!
2点ABの中点は、腹になる(強め合いの点)になることがわかっているので、半波長を図に描き込んでみましょう。
この後は、AB間にどれくらいの半波長が入るか考えていくよ!

AB間の距離は、1.7\(\lambda\)で、半波長の長さが0.5\(\lambda\)だから、AB間に入る半波長の数は
$$1.7\lambda÷0.5\lambda=3.4個$$
となります。
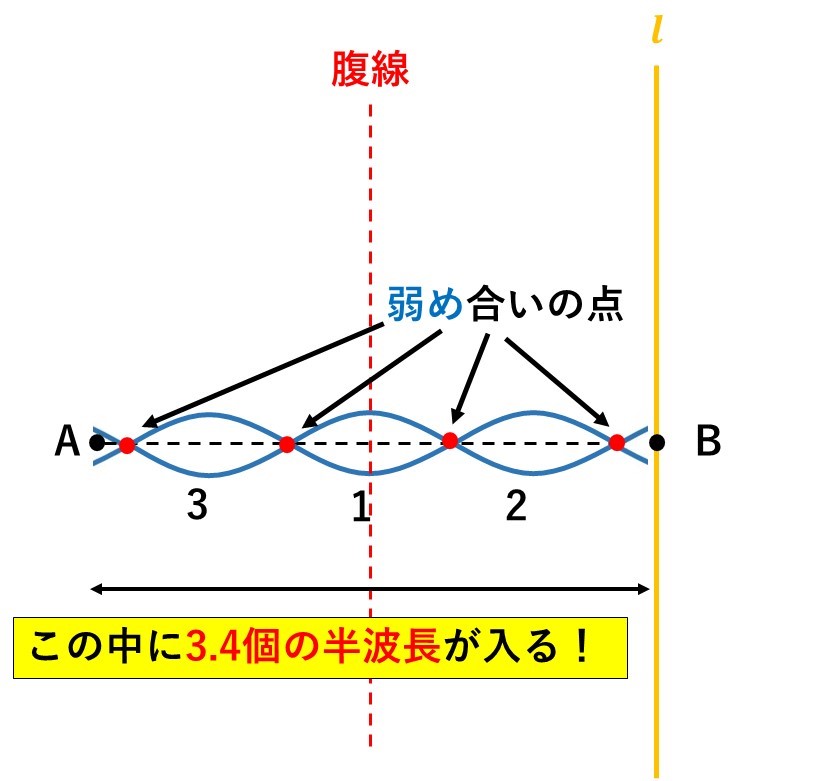
もうすでに、真ん中には半波長が1個入っているので、残り2.4個を上のように入れてあげましょう!
すると、勝手に弱め合いの点が出てきますので、その点を通るような双曲線を書けば、おしまいです。

波の干渉図は、双曲線になることも前回やりました!
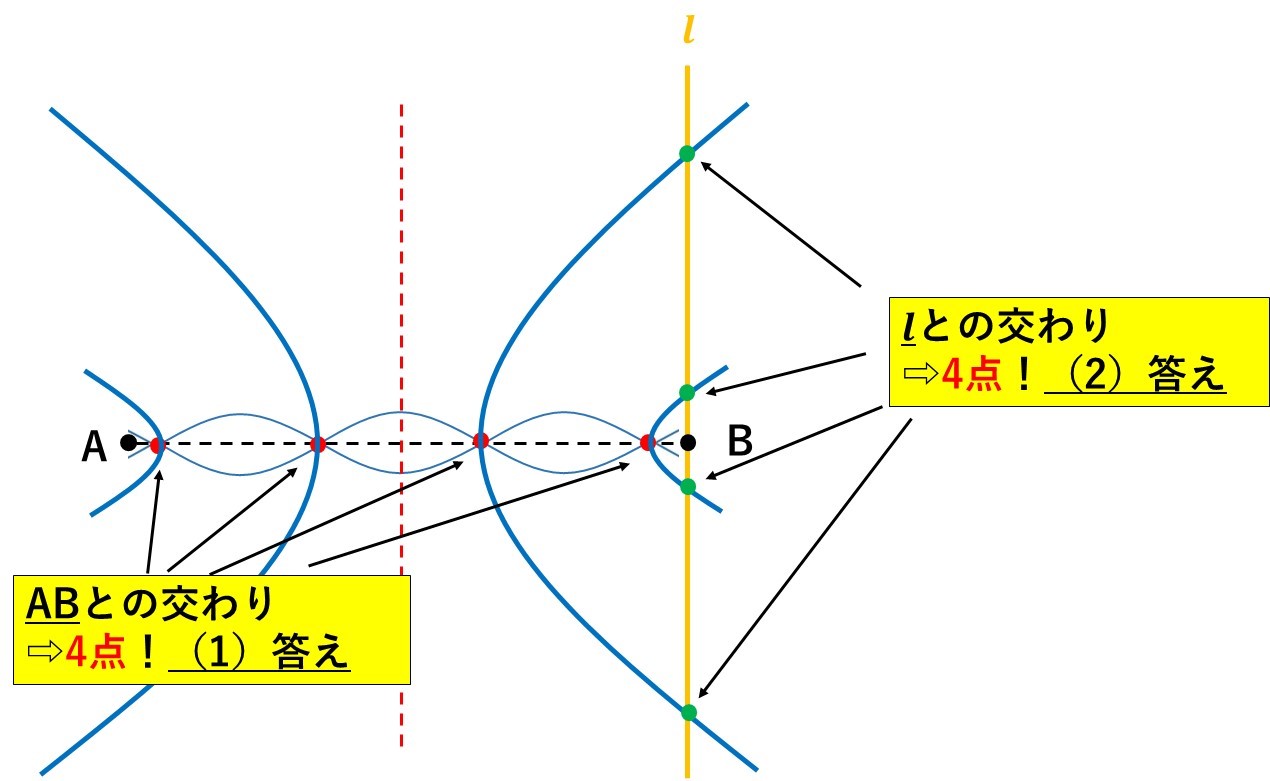
双曲線を描くと、直線\(l\)と4か所で交わることがわかります。
よって、答えは上のようにいずれも『4点』となります。
【例題2】波の干渉問題
例題

直線\(l\)と弱め合う線(節線)との交わる点の個数を求めよ。ただし、波源Aと壁の距離は\(\lambda\)である。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
今度は、壁があるけどどうすればいいかな?

解答:波の干渉問題
波の干渉の問題で、壁があるときは、壁に対して波源の『対称点』を取って考えましょう!

ここまでくれば、後はひとつ前の問題と同じように解くことができます!
波源AA'の距離は、2\(\lambda\)なので、
半波長は2\(\lambda÷0.5\lambda\)=4個入ることがわかりますので、半波長を描き込んで、双曲線を描くと下のようになります。
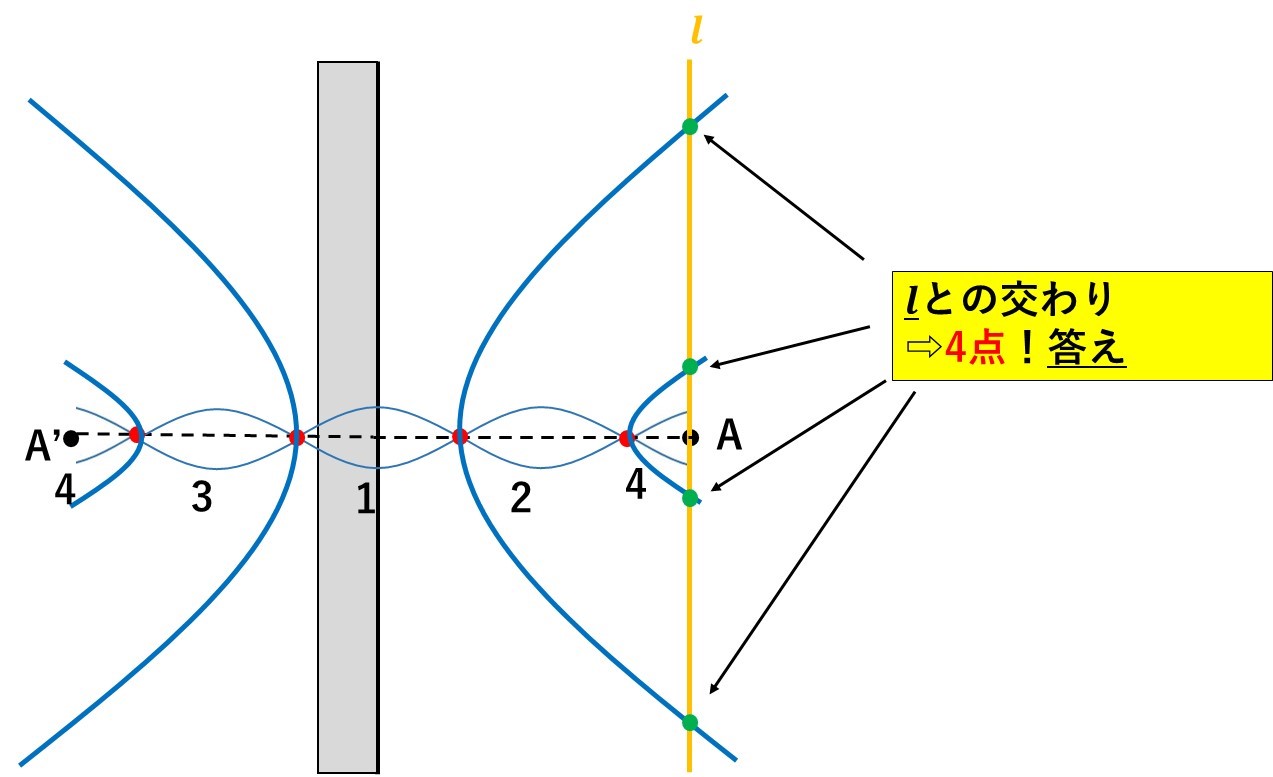
上の図をみると、直線\(l\)とは4点で交わっていることから、答えは『4点』となります。
まとめ:波の干渉は絵を描いて視覚的に求めるのがコツ!
今回は、波の干渉の問題の解き方について話してきました。
解き方についてまとめると、以下のようになります。
ココがポイント
➁同位相波源であれば、2点の中点は腹になるので、半波長の腹と一致するように図を描く!
➂➀で求めた数の波長を描き込み、双曲線を描く
このステップさえできれば、問題は解くことができますので、自分が持っている問題集を使って解いてみましょう!


