・原子物理ってなんだか難しそうだし、入試にも出にくいから丸暗記でいいのかな?
・光電効果とか光量子仮説とかいきなり無理です。。
こんな悩みを解決します。
本記事の内容
- 光電効果は光を当てると電子が出る現象
- 【簡単】光量子仮説をざっくり解説
- 仕事関数は金属が出るのに必要な最小エネルギーのこと

さて、ここから原子物理の範囲に入っていきます!
「原子物理って範囲少ないし入試にも出にくいから丸暗記でいいのでは?」と思っている人も多いはず。
でもそれは間違いで、原子物理は今までの範囲をしっかり理解できていればほとんど覚えることはないくらい簡単な分野です。

今までと同じようにわかりやすく物理を紹介していくので、一緒にがんばっていきましょう!
目次
光電効果とは金属から電子が飛び出す現象のこと

20世紀になり、金属板に光を当てると、金属板から電子が飛び出すことが実験から判明しました。
この現象のことを光電効果といいます。
そして、このとき飛び出た電子のことを光電子といいます。
光電効果:金属板に光を当てると、金属板から電子が飛び出すこと
光電子:光電効果で飛び出た電子
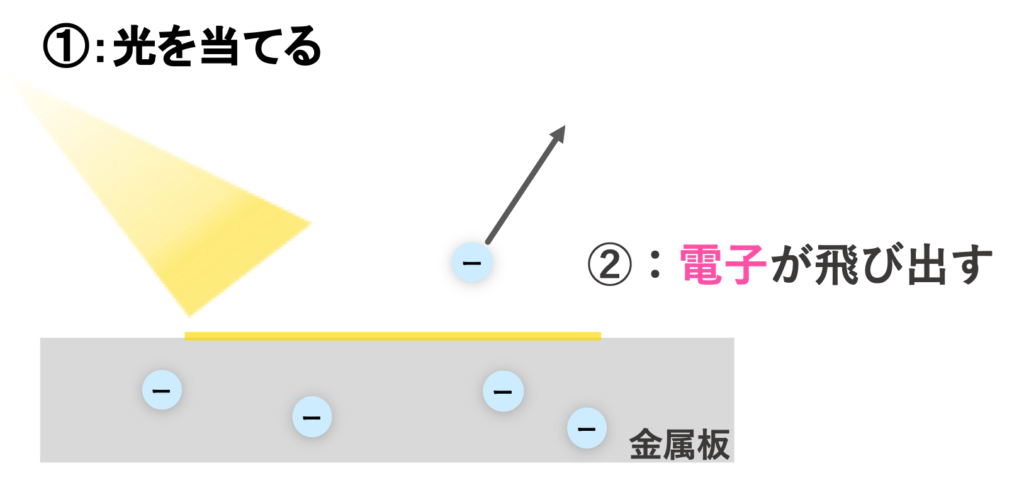
光電効果の図

まずは上の2つを覚えておきましょう!
光電効果で光電子を出すにはある条件が必要
次に、当てる光によってどんな違いがあるか調べました。
具体的には「赤い光」と「紫の光」の2つを当てたところ、紫の光しか電子が飛び出さないことが判明したのです。
| 光の種類 | 電子が飛び出る | 光の波長 | 光の振動数 |
| 赤色の光 | × | 長い | 小 |
| 紫色の光 | ○ | 短い | 大 |
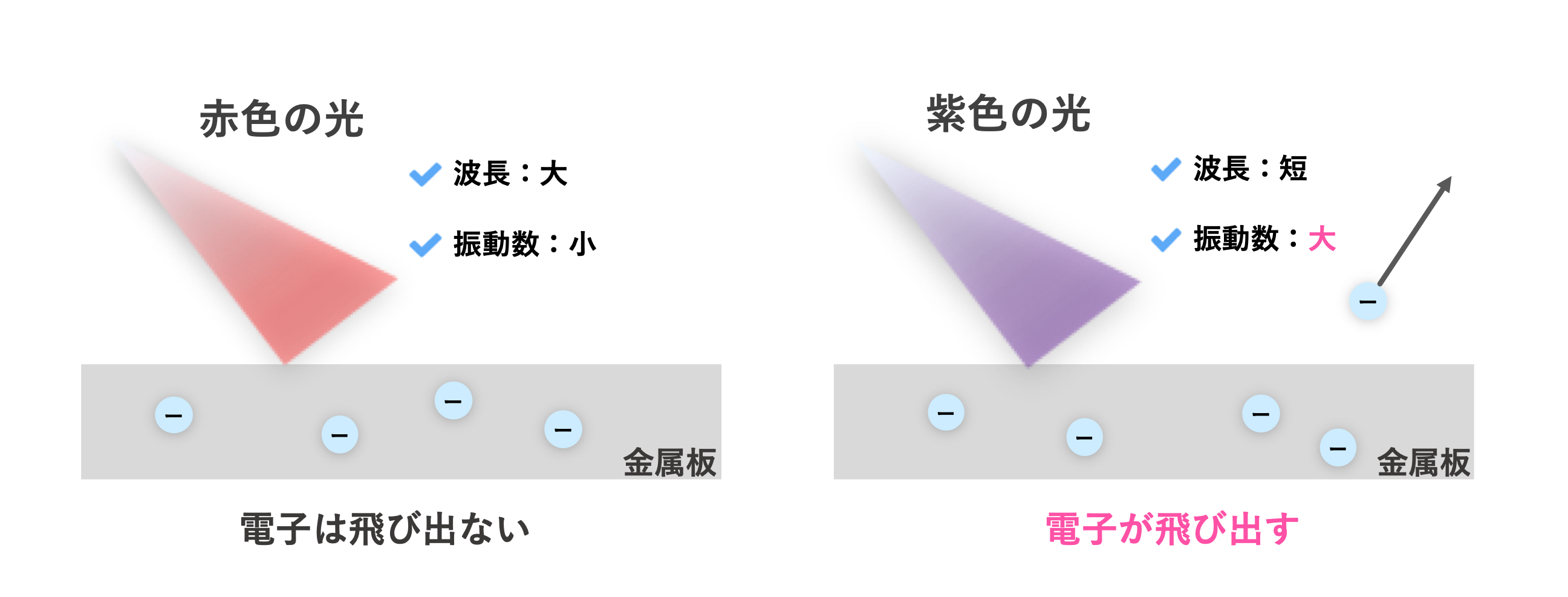
そして、電子が飛び出すには振動数が一番重要であることが判明しました。
ここを押さえる!!
- 振動数\(\nu\)が\(\nu\)>\(\nu_{0}\)(限界振動数)でないと、どんなに強い光を当てても電子は出ない
- 飛び出た電子の運動エネルギーは光の振動数のみに比例する
- 飛び出る電子の個数は光子の数(明るさ)に比例する
電子が金属からギリギリ飛び出すのときの振動数を、限界振動数\(\nu_0\)といいます。
(あとでもう一度出てくるので、必ず覚えておいてください!)
「赤い光はどんなに強く光を当てても」電子が飛び出さなかったのに対して、紫色の光は暗くても光電効果が起こったんだ!


普通明るくなれば、たくさんエネルギーがあってたくさん電子が飛び出しそうなのに不思議です。。。
もし光が波なら「光が明るい=波の振幅が大きい」ということだから、君の言うとおりエネルギーは大きくなるはず!

波のエネルギーの大きさは、振幅で決まります。(高い波ほどエネルギーを持つ)
もし光が波なら「明るい光(=振幅が大)」になればなるほど高エネルギーになるので、その分電子もたくさん金属から出るはず。
しかし、明るい光を当てても電子が飛び出なかったことから、光は波ではなく粒子としての性質も持つのでは?と仮説が出たのです。
アインシュタインの光量子仮説とプランク定数

アインシュタインは「光は波だけではなく粒子としての性質をもつ」という仮説を立てました。

光は光速\(c\)で動く粒子であると考え、これを光子と言うよ!(光子の質量は0)
光子のもつエネルギーと運動量は、以下のような式で書くことができます。
アインシュタインの光量子仮説
- 光子のエネルギー:
$E=h\nu$ - 運動量:
$P=\frac{h\nu}{c}$
※\(c\)は光子の速度、\(\nu\)は光子の振動数、\(h=6.6×10^{-34}J・s\)はプランク定数
まずは、上の2つの式を覚えておきましょう。
とはいえ、光子のエネルギーは、振動数に比例するのでその比例定数を\(h\)としているだけ(\(y=ax\)の\(a\)のようなもの)で難しくはないです!
また、光は波としての性質も持つので、波の基本式\(v=f\lambda\)を使って以下のように変形できることも覚えておきましょう。
- 光子のエネルギー:
$E=h\nu=\frac{hc}{\lambda}(\because c=\nu\lambda)$ - 運動量:
$P=\frac{h\nu}{c}=\frac{h}{\lambda}(\because c=\nu\lambda)$
上の式をもとに、光電効果を実際に式で考えてみましょう!
光電効果を式で考えてみよう【仕事関数とは?】
光電効果は、金属板に光を当てることで電子が飛び出す現象でした。
電子が金属板から飛び出す流れは、以下の3ステップです。
その②:電子が受け取ったエネルギーで仕事\(w\)をして金属表面に移動する
その③:残ったエネルギーで運動エネルギー\(\frac{1}{2}mv^{2}\)を持つ
つまり、電子と光子のエネルギーのやり取りは以下のようになります。
$h\nu=w+\frac{1}{2}mv^{2}$
(光子のエネルギー)=(表面に出るのに必要なエネルギー)+(運動エネルギー)

イメージとしては、親から1,000円もらって、電車の移動に600円使って残りの400円でタピオカを買ったみたいな感じです←
このとき、同じ光の量でも電子が深いところにあれば\(w\)がたくさん必要ですし、逆に浅いところであれば\(w\)はそこまで必要ありません。
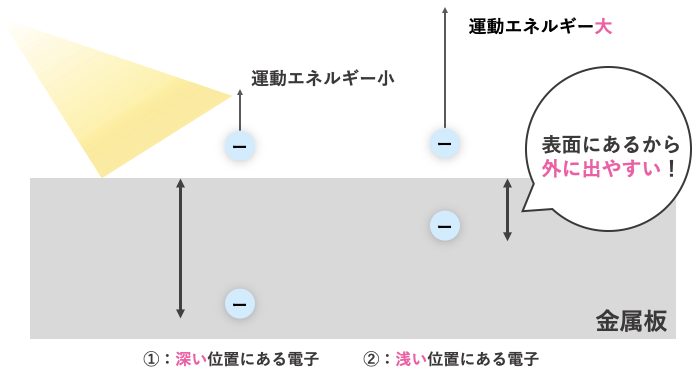
電子のある位置で使うエネルギー量が変わる
つまり表面にある電子は、金属板から飛び出すエネルギーの量が最小で済むんだ!

このエネルギーを仕事関数\(W\)といい、この値は金属の種類によって決まります。
仕事関数:金属を飛び出すために必要な最小のエネルギーのこと
飛び出すのに必要なエネルギーが最小で済むなら、飛び出た電子の速度はほかの電子と比べて最大になります。

なるほど!つまり、最表面にある電子が飛び出すときに1番速度を持つのですね!
上のことを踏まえて、式で考えると以下のようになります!
$h\nu=w+\frac{1}{2}mv^{2}$
$=W+\frac{1}{2}m{v_{max}}^{2}$
(光子のエネルギー)=(表面に出るのに最小のエネルギー)+(その分運動エネルギーは最大になる)

上の式は、意味がわかっていれば暗記しなくても書けるはず!
【疑問】限界振動数と仕事関数の関係
最後に、仕事関数と限界振動数について理解を深めます。
限界振動数\(\nu_0\)は、電子が金属からギリギリ飛び出すのときの光の振動数でした。
これを光電効果の式を考えてみましょう。
$h\nu=w+\frac{1}{2}mv^{2}$
(光子のエネルギー)=(表面に出るのに必要なエネルギー)+(運動エネルギー)
光子のエネルギーが\(h\nu_0\)のとき、電子は金属表面にギリギリ出てくることができます。
電子が金属表面に出てくるときの最小エネルギーってなんだっけ?


あ!仕事関数ですね!
正解!このとき、光子が持っていたエネルギーが、金属から出てくるためだけに使われるので、出てきたあとの速度(運動エネルギー)は0になります!

つまり、光電効果の式は以下のようになりますね。
$h\nu_0=W+0$
(光子のエネルギー)=(表面に出るのに必要なエネルギー)+(運動エネルギー)
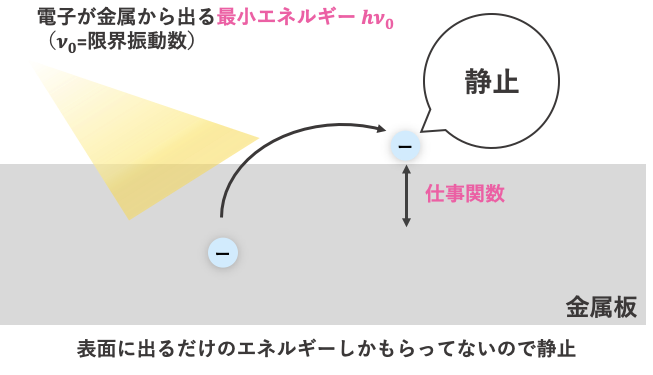
限界振動数と仕事関数の関係図
上の関係式を暗記するのではなく、言葉の定義から関係を導き出せるようにしておきましょう。
まとめ:光電効果や光量子仮説は言葉と現象を理解すれば難しくない

今回は、光電効果と光量子仮説についてお話ししました。
原子物理は、物理現象と言葉の定義を覚えればだれでも簡単に解けるようになります。
次の記事では、実際に光電効果を使ったグラフの問題を解いていくので合わせてやっていきましょう。
今回は以上です。
関連記事