
・波の干渉条件の公式がわからない
・公式ってどーやって作られてるの?
・覚えなくてもいい方法を知りたい
波の干渉の式、『強め合いの式』『弱め合いの式』2つありますが、偶数倍とか奇数倍とかややこしいですよね。
僕も実際に高校生の頃、公式の意味が分からなくて、波の干渉が大嫌いでした。
ですが、波の干渉条件の式は、原理さえ理解してしまえば、難しいことは一切なく、どんな問題でも解くことができるようになります。
そこで今回は、『波の干渉条件』の公式について、詳しく話していきます。
この記事を読めば、干渉条件の問題は簡単に解けるようになりますので、ぜひ最後まで見ていってくださいね。
✔この記事の内容
・波の干渉の式の求め方
・干渉図は双曲線になる
✔この記事の信頼性
浪人時に苦手だった物理を、記述模試偏差値65以上、センター試験満点近くまで伸ばした『考え方』や『解き方』について、大切なエッセンスを『ぎゅっと』凝縮してまとめています。
波の干渉とは強め合ったり弱め合ったりすること!

そもそも波の干渉とは、複数の波が重なって、波同士が波を強め合ったり弱め合ったりする現象のことを言います。
具体的に説明すると、『山と山』『谷と谷』同士がぶつかると強め合い、逆に『山と谷』がぶつかると波は弱められます。

同位相波源での波の干渉
それでは、実際に波の干渉の式を導いていきましょう!

先生、同位相波源って何ですか?
ある2点から波を起こしていくんだけど、どちらも同じ形で始まる波を、同位相波源というよ!


まずは、点Aから点Pに伝わる波を考えます。
波の形を見ると、点Pでは山になっていることがわかりますね!

ここまでは大丈夫です!

次に、点Bから同位相波源を発生させると、波の形、波の始まり方が同じ(同位相波源)なので、点Pでは山と山が重なり、強め合います!
では、点Bが作る波が、点Pで山を作るのは、この場所だけでしょうか。

これを考えるには、A,Bで作られる波が同位相波源、つまり2つの波は同位相で出発していることが大切です!
同位相波源では、Aが山で出発するならBも山で、Aが谷で出発するならBも谷で出発しなければいけないのです。
この図ではAが『山と谷の折り返し地点』で出発しているので、Bも『山と谷の折り返し地点』で出発します。

『山と谷の折り返し地点』となる部分は無限にありますが、そのどれかに点Bを取ることで、点Pでは山ができて波が強め合うのです。
つまり、点Aで作る波と同じ形になる場所が、Bの波源になるということだね!

では、この点Bはどのような位置に現れるのか、波の波長の関係から見ていきましょう。

波の波長とは、『波のウェーブ1個分の長さ』のことです。
点Aから点Bが現れる距離を見てみると、波長の整数倍になっていることがわかります。
このAPとBPの差のことを、経路差といい、この経路差が波長の整数倍になるときに、波は強め合うことがわかります!
ココがポイント
この言葉を式にすると、整数mを使って
$$|AP-BP|=m\lambda$$
となります。
公式は覚えないで、言葉と原理を説明できるようにしておくことが大切だよ!

【干渉条件】波が弱め合う条件
次は、点Pにて波が弱められる条件について考えていきましょう。
そもそも波が弱められる条件は、『山と谷が重なるとき』でしたね!

それでは、点Bはどこにあればいいでしょう。

さっきと一緒で、同位相波源だから、AとBからは同じ形の波が出されます。
Aから出される波の形を見ると、右上がりの波の形をしているので、Bが出す波から同じ形を探すと、上の図の2か所がみえますね!
ABの経路差が$$((整数)+\frac{1}{2})\lambda$$
となっているときに、点Pにおいて波が弱め合うことがわかりますね!
強め合い弱め合いの線は双曲線なる

同位相波源において、強め合い、弱め合いの式は下のように書けました!
ココがポイント
【弱め合いの式】$$(経路差)=((整数)+\frac{1}{2})×\lambda$$
じゃあ、2つの式の共通点はなにかな?


うーん、2つとも経路差が、波長の何倍かの定数で表されていることですか?
正解!経路差は、2定点からの距離の差のことだから、それが一定になっているってことだね!

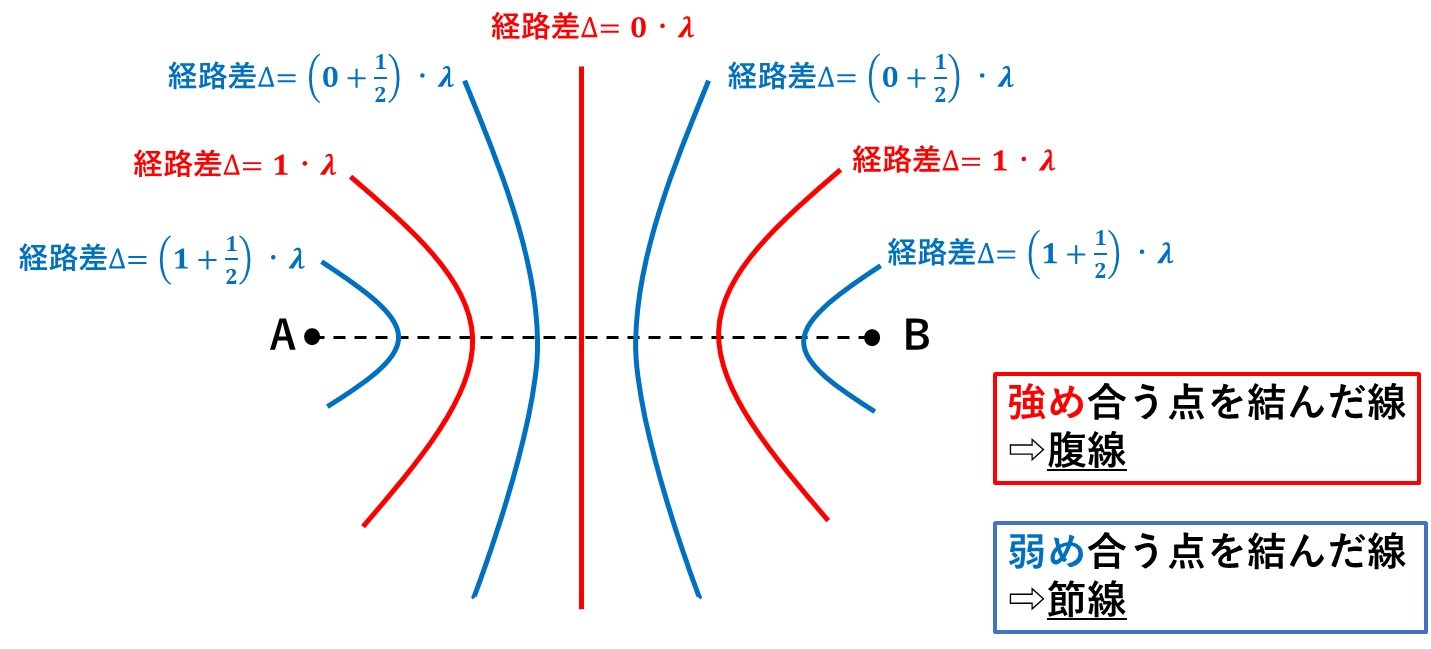
強め合い、弱め合いの点をそれぞれ結んだ線は、『2定点からの距離の差が一定』である点の集まりになります。
上のように、2定点からの距離の差が一定の点の集合体は、『双曲線』を描くことが知られています!

AとBを結んだ中点Pは、経路差AP-BPが0になるので、上のように$$(経路差)=0×\lambda$$と表すことができます。

てことは、同位相波源のとき、2点の中点は必ず強め合いの線(腹線)ですね!

そして、強め合いの線と、弱め合いの線は交互にやってくるので、真ん中の腹線から、左右に『整数が0の弱め合いの線』『整数が1の強め合いの線』『整数が1の弱め合いの線』・・・と続いていきます!
自分で作図するときも、2点の中点を見つけて、そこから広がるように作図していけば簡単だね!

まとめ:干渉条件は図と公式両方で理解するのがコツ

今回は、波の干渉の公式について話してきました。
ココがポイント
【弱め合いの式】$$(経路差)=((整数)+\frac{1}{2})×\lambda$$
公式を覚えることも大切ですが、それよりも『どうしてこの式が出てくるのか』ということがわかることが大切です!
公式を覚えるだけでは、MARCH以上の問題に対応できなくなってしまうので、自分で導出できるようにしておきましょう。

