
・交流問題の解き方がわからない
・参考書を見ても問題が解けない
交流の問題ってめちゃくちゃ難しいですよね。
高校生の時は、いくら勉強しても交流の問題が解けるようになりませんでした。
ですが、勉強していくうちに、交流の問題は『たった2つの解き方しかない』ことに気が付きました。
そこで今回は、参考書に書いてない交流問題の解き方について、例題とともに紹介していきます。
この記事を読めば、交流回路の解き方がわかるので交流問題でつまずくことはなくなりますよ。
前回の記事は交流を完全理解!!コイルの位相はπ/2だけずれる理由をわかりやすく導出!を参考にどうぞ。
✔この記事の内容
・交流回路の解き方
・交流回路の例題とインピーダンス
✔この記事の信頼性
浪人時に偏差値65以上センター試験満点近くまで伸ばした僕が、参考書には書かれていない考え方や勉強法について、凝縮してまとめています。
【電磁気の分野の注意点】
極力微積は使わないように説明していますが、電磁気の分野では微積を使うことで理解が深まる場所は、微積を使っています。
微積といっても、数Ⅱ数Ⅲの教科書例題レベルなので、身構えなくても大丈夫です!
【例】
・\(v=\frac{dx}{dt}\)
・・・(分子)の(分母)変化と読む。今回は、(位置)の(時間)変化なので、速度のこと
・\(a=\dot{v}=\ddot{x}\)
・・・ドットで微分を表す。2回微分であれば、ドットの数は2つ。
交流回路の解き方はたった2つ!

結論、交流回路の問題の解き方はたった2つです。
交流回路の解き方
➁電流・電圧を最大値で置いて、位相のずれを考えてベクトルで解く!
解き方は、上の2通りあるのですが、今回は➀の微積の知識を使って解くやり方について、紹介していきます。
ベクトルを使った解き方は交流回路をベクトルを使って解く方法を参考書よりもわかりやすく解説を参考にしてみてください。

微積嫌なんですけど、、
➁の方法を使えば、微積は必要ないんだけど、電磁気の範囲に関しては微積を使った方が理解が深まるから、➀もできるようにしておくといいよ!

微積といっても、数Ⅱ数Ⅲの教科書レベルの問題ができれば、余裕で解けるレベルなので、心配はいりませんよ!
それでは、まず並列交流回路の問題を解いていこう!
例題:RLC交流回路
例題
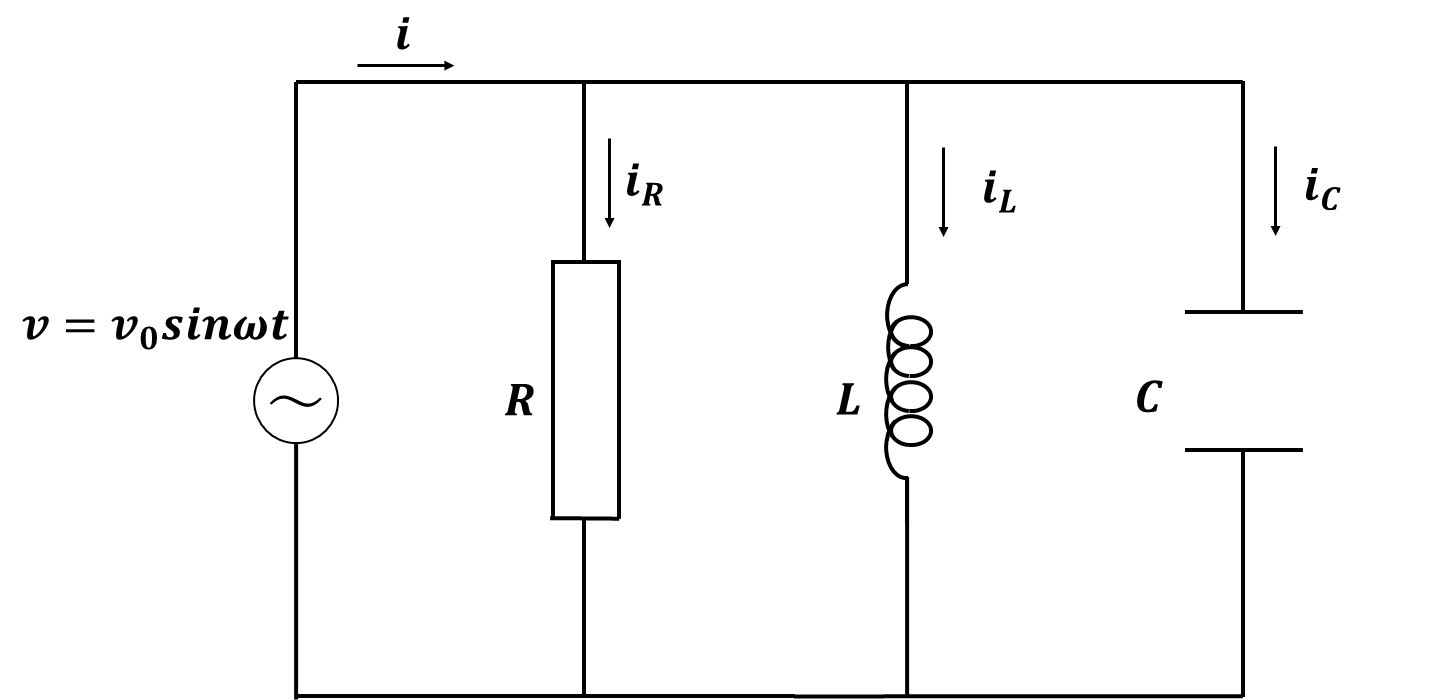
上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。
(1)\(i_R,i_C,i_L\)を求めよ。
(2)回路全体のインピーダンスZを求めよ。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは、解説していきます。

(1)の解答
例題

上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。
(1)\(i_R,i_C,i_L\)を求めよ。
交流でも直流でも、回路問題の解き方は『手順』が決まっていました。
回路問題の解き方
➁オームの法則を使って抵抗にある未知数を求める
➂回路方程式を立てて、電荷や電流を求める
※回路方程式とは、キルヒホッフの法則(電流保存、電位1周で電位差0)や電荷保存の式のこと
今回は、コイルもあるので、仮定した電流とは逆向きに誘電起電力\(L\frac{di}{dt}\)も描きましょう!
【頭の使い方】
➀電流は問題文で仮定されているので、コンデンサーの電荷を\(q\)と仮定する。
➁抵抗があるので、そこにかかる電圧をオームの法則を使って求める。(同時に、コイル、コンデンサーの電圧も描いてしまう)
➂電流保存は、枝分かれから、全体を流れる電流\(i\)を、\(i_R,i_L,i_C\)を使って書く。(電荷保存はコンデンサーが2個以上無いので使わない)
上でたくさんのことをやっていますが、すべて描き込むと大したことはありませんよ!

さて、最後に➂の『電位差1周で0』(キルヒホッフの第二法則)を使うと、電源電圧を含むループが3つあるので、式は
$$v_0sin\omega t=Ri_R・・・➀$$$$v_0sin\omega t=L\frac{di_L}{dt}・・・➁$$$$v_0sin\omega t=\frac{q}{C}・・・➂$$
となります。
さらに、コンデンサーがあるので、電荷保存の式(時間変化ver)も書いて
$$i_C=+\frac{dq}{dt}・・・➃$$
となります。
交流コンデンサーの導出で、電荷保存の式(時間変化ver)を使わないと解けなかったから、今回も式を書いたよ!導出が大事って意味わかったかな?

$$v_0sin\omega t=Ri_R・・・➀$$$$v_0sin\omega t=L\frac{di_L}{dt}・・・➁$$$$v_0sin\omega t=\frac{q}{C}・・・➂$$$$i_C=+\frac{dq}{dt}・・・➃$$
ここからは、交流の導出のときを思い出しながら、まったく同じように解いていきます。
まずは、➀より$$i_R=\frac{v_0sin\omega t}{R}・・・答え$$
➁式を積分すると、$$L\frac{di_L}{dt}=v_0sin\omega t・・・➁$$$$\int{L\frac{di_L}{dt}}dt=\int{v_0sin\omega t}dt$$$$i_L=-\frac{v_0}{\omega L}cos\omega t・・・答え$$
➂式の\(q\)を➃式に代入して、$$v_0sin\omega t=\frac{q}{C}・・・➂$$$$i_C=+\frac{dq}{dt}・・・➃$$
$$i_C=\omega Cv_0cos\omega t・・・答え$$
となります。
計算過程がわからない人は、各交流回路の導出の記事を、確認してみよう!

(2)の解答
例題

上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。
(2)回路全体のインピーダンスZを求めよ。
ココがポイント
交流回路の抵抗であるインピーダンスは、『実効値』か『最大値』を使って、以下のように表せました。
インピーダンスの求め方
実効値は、電流あるいは、電圧の最大値を\(\sqrt{2}\)で割ったものになりますので、いずれにしても最大値を求める必要があります。
電圧の最大値は、電源電圧$$v=v_0sin\omega t$$の\(v_0\)なので、電流の最大値を求めてしまえば、インピーダンスを求めることができます。

回路全体の電流は、$$i=i_R+i_C+i_L$$なので、(1)で求めた答えを代入していくと、
$$i=i_R+i_C+i_L$$$$=v_0\left\{\frac{1}{R}sin\omega t+\left(\omega C-\frac{1}{\omega L}\right)cos\omega t\right\}$$
電圧の最大値は、sin関数の最大値だったから、電流もsin関数に直して、統一させる必要があるね!


ここから、sin関数に直す方法・・・
数Ⅱで習う『合成』を使うんだ!

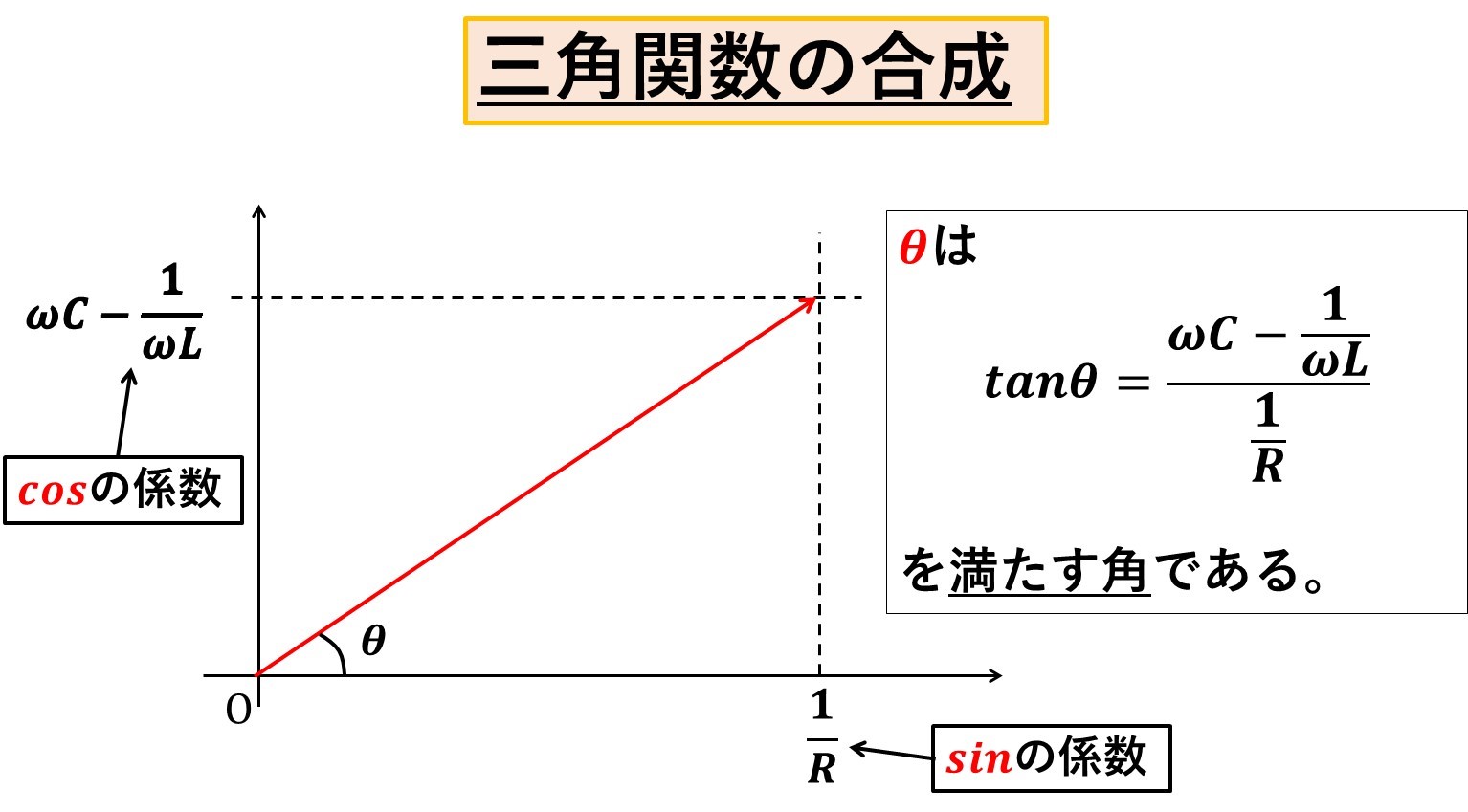
合成すると、
$$i=v_0\left\{\frac{1}{R}sin\omega t+\left(\omega C-\frac{1}{\omega L}\right)cos\omega t\right\}$$$$=v_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}sin(\omega t+\theta)$$
最大値は、sin関数の前にある部分になるので、回路全体を流れる電流の最大値は$$v_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}$$
となります。

最後は、インピーダンスの公式を使っておしまいですね!
電圧の最大値\(v_0\)と、電流の最大値\(v_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}\)を
$$Z=\frac{v_0}{i_0}$$に代入して、
$$Z=\frac{v_0}{i_0}$$$$=\frac{1}{\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}}・・・答え$$
となります。
インピーダンスは、抵抗みたいなものだから、直列回路と同じように、回路全体の電流と電圧を求めればいいという方針になるね!

まとめ:交流回路は解き方を覚えれば簡単!

今回は、交流回路を微積を使って解いてきました。
やったことは、たった3つです。
ココがポイント
➁基本的な微積の計算をする!
➂インピーダンスを出すために三角関数の合成をする!
結局、交流は『直列回路』と『微積や合成などの基本的な数学』の知識があれば、同じように解けるということです。
なので、交流回路ができない人は、上のいずれかが苦手な可能性があるので、復習して苦手を解消しましょう。
今回は以上です。
関連記事交流回路をベクトルを使って解く方法を参考書よりもわかりやすく解説


