
・どうして、点電荷の電位の式に、マイナスが付くのですか?
・電位の基準を、無限遠点にとるのはなぜ?
この疑問をもつ人は、あなただけではなく、物理をやったことがある人すべてに共通する疑問なのです。
そこで今回は、公式の丸暗記をしないで、点電荷の作る電位について詳しく理解していきます!
⇩こちらの記事をまだ読んでいない方は、先にこちらを読むことをおすすめします!
合わせて読みたい!
一様でない場での電位(マイナスが付く理由)

一様でない電場は、点電荷によって作られ、その大きさは距離と電荷の大きさに依存して、
$$E=k\frac{Q}{r^2}$$
と書けます。
この空間においての、電位(+1[C]あたりが持つ静電気力による位置エネルギー)は、、
電場を作っている点電荷が、プラスの電荷\(+Q\)なら
$$E=k\frac{Q}{r}$$
になり、逆に電場を作っている点電荷が、マイナスの電荷\(+Q\)なら
$$E=-k\frac{Q}{r}$$
と書けますね。
どうしてこのような公式になるのか、詳しく見ていきましょう。
点電荷の作る電位の導出

電位は、『電場を作っている電荷の符号』によって変わるのですか?
そうだね!どうしてそうなるのか見ていこう!

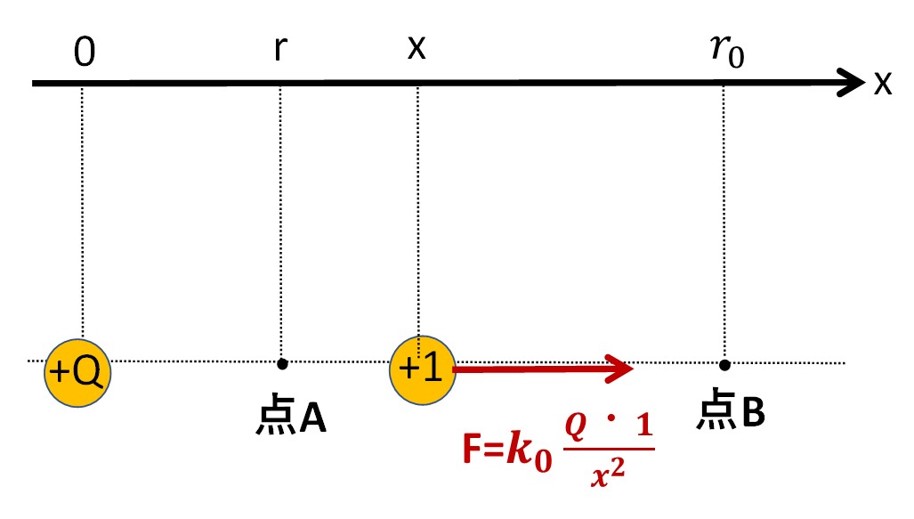
軸を右向きにとって、0の位置に\(+Q\)を固定します。原点から距離rのところをA点、\(r_0\)の点をB点とし、電位の基準とします。
次に、点Aに+1[C]を置き、手を離すと+1[C]はクーロンの法則より、\(+Q\)から静電気力
$$F=k\frac{+Q・+1}{x^2}$$
を受けどんどん離れて、A点からB点に移動します。

力学のときの話を覚えていますか?
『基準に戻るまで』に『重力』が\(mg・h\)の仕事をする能力のことを『位置エネルギー』といったのです。

同じように考えると、点Aにおける電位(位置エネルギー)は、『基準に戻るまで(点A→点B)』に『静電気力』がする仕事と等しく、
$$V=\int_r^{r_0}k\frac{+Q・+1}{x^2} dx$$
となります。

わわわ!積分が出てきた・・・
電場の大きさが場所によって違うから、静電気力も場所によって違うよね。力の大きさが変わるときの仕事は、(力)×(距離)ではなく積分を使うしかないんだ。


こんな積分やったことありません!
大丈夫!変化するのは分母にある\(x^2\)だけだから、\(\frac{1}{x^2}\)を\(x^{-2}\)にして積分してごらん!


あ、なんかできそうです!
$$V=\int_r^{r_0}k\frac{+Q・+1}{x^2} dx$$
$$=\left[-kQ\frac{1}{x}\right]^{r_0}_r$$
$$=\frac{-kQ}{r_0}+\frac{kQ}{r}$$
となります!
これが、基準を\(r_0\)にとったときの電位です!このままの形では、電位の式が長くて使いづらいですよね。

あ!だから位置エネルギーの基準を∞にとるんですね!
その通り!基準の\(r_0\)を∞に変えると、分母が∞になってその項は0とみなすことができるんだ!

$$V=\frac{-kQ}{r_0}+\frac{kQ}{r}$$
$$=\frac{-kQ}{∞}+\frac{kQ}{r}(r_0を∞にする)$$
$$=0+\frac{kQ}{r}$$
$$=\frac{kQ}{r}$$
これが、∞遠点を基準にとった、点電荷が作る電位の大きさになります!
式を見ると、電位の符号はプラスになっていますが、理由は計算過程を見ればわかりますが、プラスの電荷を原点に置いたからです!
逆に、原点にマイナスの電荷を置くと、点Aでの電位は
$$=-\frac{kQ}{r}$$
となります!
つまり、電位は『誰がその空間を作っているか』によって符号が変わるのです。
まとめ:電位の基準がマイナスになる理由を理解して物理の理解を深めよう!

今回は、力学と比較しながら、点電荷が作る電位にマイナスが付く理由について、紹介してきました!
前回の記事と今回の記事で、電位については網羅して説明しましたので、ノートにまとめて整理してから、問題集を解いて理解を深めてください。
また、今回積分を使って証明しましたが、これから先でも積分を使った導出をしますので、不安な方は数学Ⅱをよく復習しておいてくださいね!
今回は以上です。
関連記事電気力線は+1[C]の動いた道筋だった?!ガウスの法則につながる電気力線の話



