・ドップラー効果って何?
・問題の解き方がわからない
・ドップラー効果が起こる原理って何?

こんな悩みを解決します。
受験生の中でも、ドップラー効果が苦手な人は、多いのではないでしょうか。
実際に僕も高校生のときは「公式丸暗記」で、難しい問題はまったく刃が立ちませんでした。
実は、ドップラー効果の公式を正しく理解できれば、めちゃくちゃ簡単に解くことができます。
そこで今回は、ドップラー効果の公式の使い方や導出について紹介していきます。
この記事を読めば、『ドップラー効果の公式の使い方がわからない』『導出ができない』なんてことはなくなりますよ。
✔この記事の内容
・そもそもドップラー効果とは
・現象が起こる2つの原因
・受験生の8割が知らない公式の使い方
✔この記事の信頼性
浪人時に苦手だった物理の偏差値を65以上にまであげた、物理の勉強法や参考書に書いていない問題の解き方について紹介しています。
目次
ドップラー効果が起こるのは振動数が変化するから

『ドップラー効果』とは、音源から出る音の数が、何らかの原因で変化する現象のことを言います。
音の数のことを「振動数」と言いますが、振動数が変化してしまう原因は、2つだけです!
【振動数が変化する原因】
➀音源が動いて波の波長が変化する
➁観測者が動いて音の相対速度が変化する
なんだか、難しそうですね。

それじゃ、もう少し簡単に考えてみよう!

あなたは、今ボーリング場にいるとしましょう。


振動数は、1秒間に出せる波の個数なので、今回は、1秒間にボーリングの球を10個出せるとします。

音源は、1秒ごとに、違った色のボーリングの球を投げまくりますが、観測者も、1秒間に音源が投げた分のボーリングの球と同じ数だけ受け取ります!
今回は、わかりやすいように波(ボーリングの球)を色分けして区別しているけれど、どの色の球を受けとったかよりも、観測者と音源がどちらも1秒間に同じ数の波を受け取っていることが、重要です!

なので、今回の場合は
(1秒間に音源が出す波の数)=(1秒間に観測者が受け取る波の数)
という関係式が成り立ちます。
ドップラー効果は、振動数(受け取る波の数)が変化する現象でしたので、今回は、ドップラー効果が起こっていないといえますね。
それでは、振動数が変化する(ドップラー効果が起こる)場合を考えていきましょう。
➀音源が動いて波の波長が変化する
『波の波長』とは、波のウェーブがもとの高さに戻ってくるまでに移動した長さのことを言います。
今回の例でいくと、『ボーリングの球の間隔』に当たります。
音源が動くと、本当に波長が変化するのか見てみよう。


さっきよりも、ボーリングの球の間隔が狭くなっていますよね。
音源は、必ず1秒間当たりに、ボーリングの球を10個投げる(それが振動数)ので、自分が動いている分、ボールの間隔が狭くなってしまいます。
結果として、\(t=2\)のときに観測者が受け取った球の個数(振動数)は、音源が止まっていた時よりも多くなってしまったのです。
観測者が受け取る波の個数が変化したから、ドップラー効果が起こるとわかるね!

ココがポイント
➁観測者が動いて音の相対速度が変化する
さっきは、音源が動きましたが、観測者が動く場合でもドップラー効果(観測者が受け取る振動数の変化)が起こります。
これは、とてもイメージがつきやすいですよ!


当然ですが、ボーリングの球に自分からあたりに行くわけなので、観測者が受け取る振動数は多くなります!
よって、観測者が動く場合も、ドップラー効果が起こることがわかりましたね。
ココがポイント
【参考書に書いてない】ドップラー効果の公式には正方向がある
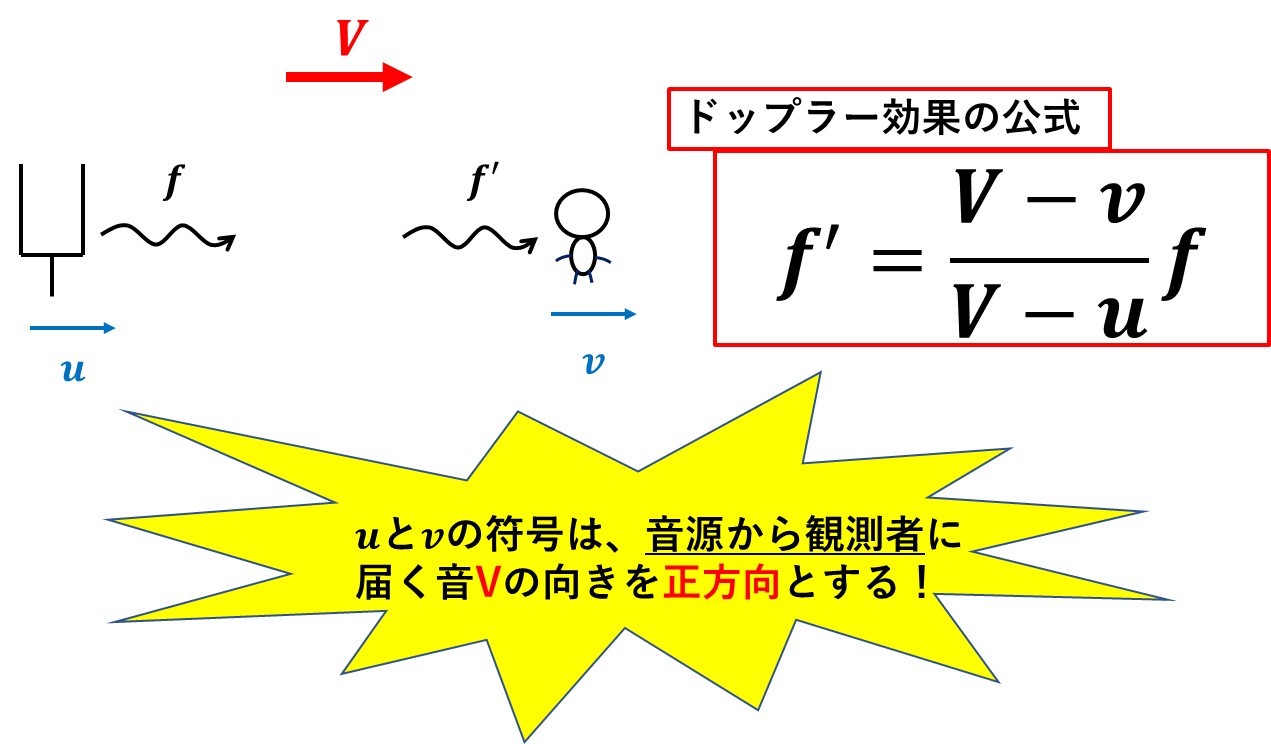
ドップラー効果で間違いが多いのは、音源と観測者が移動しているときの、速さの符号間違えです。
必ず、ドップラー効果では、音源から観測者方向を正方向として、式を立てなくてはいけないのです。
ココがポイント

例えば、上のような問題では、観測者の速さが、音源から観測者に伝わる音と逆向きなので、上のようにマイナスで代入します。
上の内容は、すごい大切なので、しっかり覚えておきましょう!
と、言われても、どうして音源から観測者に伝わる音の方向が正方向か、気になりますよね。
この答えは、ドップラー効果の導出をすればすぐにわかります!
導出といっても、そんなに難しくないから、やってみよう!

ドップラー効果の導出はできるようにしておこう!

ドップラー効果の導出は、3ステップで完結します!
【ドップラー効果の導出】
➀音源が動くことによる波長の変化を出す
➁観測者が動くことによる相対速度変化を出す
➂波の基本式に代入する
➀音源が動くことによる波長の変化を出す

『速度』とは、1秒あたりに進む距離のことなので、音は1秒間にV[m]進みます。
さらに、音源は、1秒間でu[m]進むので、図を描くと以下のようになります。


音源が動くことで、音の数は変わりませんが、1つの波の長さ(波長)が変化してしまうのでしたね。

今回、\(f\)個の波が\(V-u\)の中に入っていることから、波長\(\lambda '\)は
$$\lambda '=\frac{V-u}{f}・・・➀$$
となります!
➁観測者が動くことによる相対速度変化を出す

観測者が動くことで、観測者から見た、音の相対速度が変化するのでした。

相対速度は、(相手の速度)-(自分の速度)で求めることができるので、観測者から見た音の相対速度V'は、
$$V'=V-(-v)$$$$=V+v・・・➁$$
となります。
速度の正方向は、音が届く相対速度を求めているので、音源から観測者に伝わる方向を、正方向としています!

➂波の基本式に代入する
波の基本式は、
$$v=f\lambda$$
でした。これを変形して、➀➁の式を代入すると、
$$f'=\frac{V'}{\lambda '}$$$$=\frac{V+v}{V-u}・・・導出終わり$$
となり、導出完了です。
導出のときに、音が届く相対速度のところで、速度の正方向を決めたから、ドップラー効果の正方向は音源から観測者方向を、正方向として決めているのですね!

意外と知らない人が多いから、導出も含めてできるようにしておきましょう!

まとめ:ドップラー効果は原理を押さえれば簡単!
今回は、ドップラー効果について話してきました。
大切な内容は以下の通りです。

【ドップラー効果の導出】
➀音源が動くことによる波長の変化を出す
➁観測者が動くことによる相対速度変化を出す
➂波の基本式に代入する
ドップラー効果は、難関大はもちろん、どこの大学でも頻出ですので、導出もしっかりできるようにしておきましょう!

