【難関大頻出】弾丸が木片にささる運動量保存の問題の解き方をわかりやすく解説

悩んでる人

・弾丸の問題がわからない
・そもそもどの公式を使っていいかわからない

今回は、そんな悩みについて解決していきます。

大阪大や東工大などの旧帝大、難関国立大で頻出の弾丸問題ですが、この問題は『運動量保存則』を使って解くことができます。

現象自体は単純なので、難関大を受けない人も運動量保存則の練習問題として、ぜひ解いてみてください。

そもそも衝突問題の解き方は3つ！

実は、高校物理の衝突・分離の論点は3つしかなんだ！

塾長

つまり、衝突・分離問題の解法も上の3つに絞ることができます。

それでは、例題を解いていきましょう。

塾長

木片が刺さる弾丸問題：解き方を解説

例題

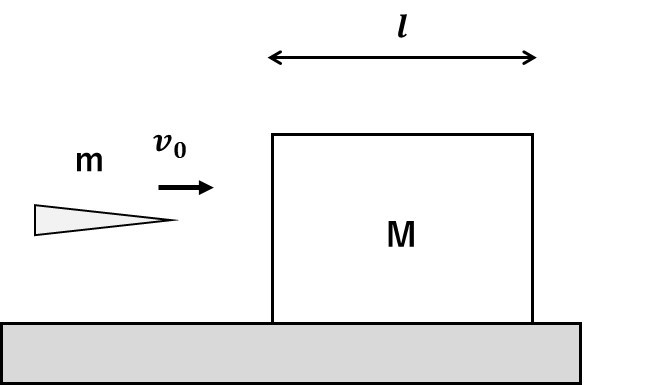
質量M、長さ\(l\)の物体を、なめらかな床面においた。この物体に、質量mの弾丸を速さ\(v_0\)で打ち込んだ。弾丸は水平線上を進み、木片から受ける抵抗力は常に一定とする。

（１）最初、木片を床面を固定して弾丸を打ち込んだところ、深さdまで入り込んだところで静止した。抵抗力Fの大きさを求めよ。
（２）次に、木片を固定せずに、再び弾丸を\(v_0\)で打ち込むと、木片に入り込み一体となって一定の速さで動いた。その時の速さをもとめよ。また、あてた弾丸が入り込んだ深さを求めよ。
（３）弾丸が木材を貫くには、初めの速さはいくら以上でなくてはならないか。
（問題引用：名門の森、大阪大）

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

それでは、解説していきますよ！

塾長

例題

質量M、長さ\(l\)の物体を、なめらかな床面においた。この物体に、質量mの弾丸を速さ\(v_0\)で打ち込んだ。弾丸は水平線上を進み、木片から受ける抵抗力は常に一定とする。

（１）最初、木片を床面を固定して弾丸を打ち込んだところ、深さdまで入り込んだところで静止した。抵抗力Fの大きさを求めよ。

この2点に着目して、エネルギー保存の式をたてると、

$$\frac{1}{2}m{v_0}^2=Fd$$$$\therefore F=\frac{m{v_0}^2}{2d}・・・答え$$

となります。

運動エネルギーが、摩擦熱に変化したとみればいいのですね！

摩擦熱は、（力）×（距離）で与えられるから、それをもとに式を立てればOKだね！

塾長

（２）の解答

例題

質量M、長さ\(l\)の物体を、なめらかな床面においた。この物体に、質量mの弾丸を速さ\(v_0\)で打ち込んだ。弾丸は水平線上を進み、木片から受ける抵抗力は常に一定とする。

（２）次に、木片を固定せずに弾丸を\(v_0\)の速さで打ち込むと、木片に入り込み一体となって一定の速さで動いた。その時の速さをもとめよ。また、あてた弾丸が入り込んだ深さを求めよ。

弾丸と、木片の衝突問題なので、上の3つの式が使えないかどうかを考えます！

弾丸と木片を物体系として考えると、外力は働かないので、運動量保存則が使えます。

弾丸と木片の間の抵抗力は、内力だからですね！

（１）とは異なり、今回は木片が固定されていません。

一体となったとき、2つの物体は同じ速さになるので、その速さを\(v\)とすると、

$$mv_0+0=mv+Mv$$$$\therefore v=\frac{m}{m+M}v_0・・・答え$$

となります。

次は、はね返り係数の式が使えるか考えます。

今回、弾丸は木片に刺さってはね返っていないので、はね返りの式は立てられません。

最後に、エネルギー保存の式を考えます。

エネルギー保存の式は、主に2点間の距離が与えられた（知りたい）ときに使いますが、今回は

の2地点におけるエネルギー保存の式を立てましょう。

求める深さをd'とすると、エネルギー保存則より

$$\frac{1}{2}m{v_0}^2=\frac{1}{2}(m+M){v}^2+Fd'$$

となります。抵抗力は常に一緒（問題文より）なので、（１）のFと、\(v\)を代入して、d'を求めると

$$d'=\frac{M}{m+M}d・・・答え$$

となります。

衝突問題はやることが決まってしまうので、簡単だね！

塾長

（３）の解答

例題

質量M、長さ\(l\)の物体を、なめらかな床面においた。この物体に、質量mの弾丸を速さ\(v_0\)で打ち込んだ。弾丸は水平線上を進み、木片から受ける抵抗力は常に一定とする。

（３）弾丸が木材を貫くには、初めの速さはいくら以上でなくてはならないか。

今回も衝突問題かつ、はね返らないので、運動量保存則とエネルギー保存則の2つを使えば解くことができます！

弾丸の初速を\(v_1\)、弾丸が突き抜ける瞬間の速さを\(u\)とすると、

運動量保存則より、

$$mv_1+0=mu+Mu$$

エネルギー保存則より

$$\frac{1}{2}m{v_1}^2=\frac{1}{2}(m+M){u}^2+Fl$$

これら2式から、\(u\)を消去すると、

$$v_1=v_0\sqrt{\frac{(m+m)l}{Md}}・・・答え$$

となります。

意外と簡単に解けました！

どういう時にどういう式を立てるか知っていれば、簡単だね！

塾長

まとめ：難関大を受ける人はしっかり問題を解けるようにしておこう！

今回は、難関大で頻出の『弾丸問題』について紹介してきました。

弾丸問題に限らず、大切なのは衝突問題・分裂問題の解き方が決まっているということです。

上の内容は、非常に大切なので、しっかりと覚えておきましょうね。