いきなりだけど、はね返り係数の公式ってどうやって覚えてる?


$$e=-\frac{{v_A}'-{v_B}'}{v_A-v_B}$$で覚えてますけど・・
このように、教科書に書いてあることが多いので、この形で覚えている人も多いですが、混乱してしまうことが多いのではないでしょうか。
実は、『はね返り係数の公式』を言葉で覚えてしまえば、簡単に公式を使えるようになります!
そこで今回は、はね返り係数の公式について理解していきます!
この記事を読めば、『問題の中ではね返り係数の公式を間違った』なんてことはなくなりますよ。
前回の記事は、以下の記事を参考にしてみてください。
関連記事力学でつまづくな!!予備校では教えてくれない力の書き方を例題とともに徹底解説
【基本】はね返り係数の公式の意味とは

そもそも、はね返りの公式を言葉で説明できるかい?


うーん、そういわれると・・
まずは下の図を見てみよう!

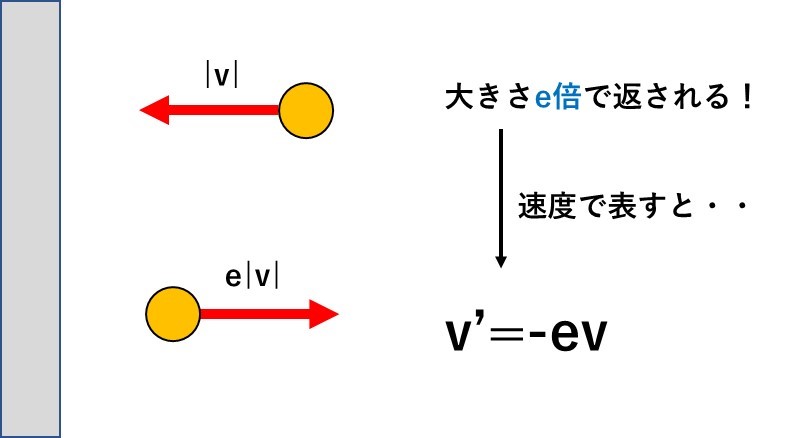
速さ\(v\)の物体が壁に衝突して、はね返ってくるときに、速さがe倍される。
これが、『はね返り係数の公式』のもとなんだ!

上の言葉の理解がすごい大切!!

また、速度で書くと、\(v'=-ev\)と書けるので、『衝突後の速度は、衝突前と向きが逆で、大きさがe倍』と説明することができるのです!
ポイント
はね返ると、『衝突後の速度は、衝突前と向きが逆で、大きさがe倍』
【導出】はね返り係数の公式
それでは、はね返り係数の公式$$e=-\frac{{v_A}'-{v_B}'}{v_A-v_B}$$を導出していきます!
導出
例題
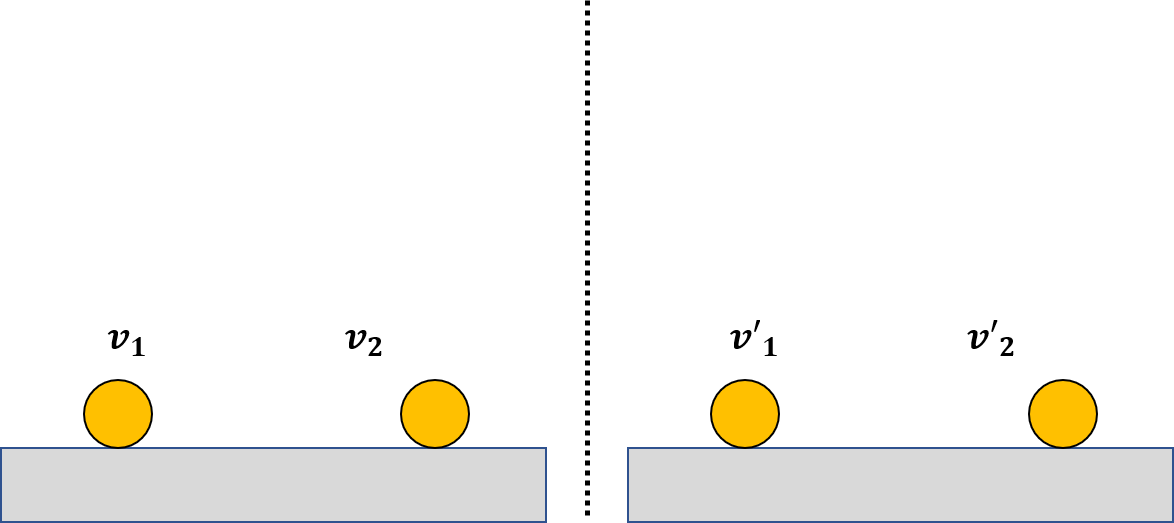
左の図のように、速度が\(v_1,v_2\)の物体が衝突して、右図のように速度が変化した。はね返り係数をeとして、はね返り係数を求めなさい。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!

はね返るときにe倍になるのはわかるけど、どっちも動いているとやりづらい、、
そんな時は、相対速度を使って、片方の動きを止めてあげればいいんだ!

※相対速度の使い方について、まだ読んでいない人は【相対速度は”相手ー自分”で考える!!はね返り係数を理解するための準備!!】をチェック!
相対速度の求め方は、『相手-自分』だったね!

相対速度
相対速度は、【相手の速度ー自分の速度】で求める!

この図のように、壁(片方が動かない)を作るには、片方の動きを止めてあげればいいのだから、下の図のようにボールの上に観測者を置いてあげればよく、
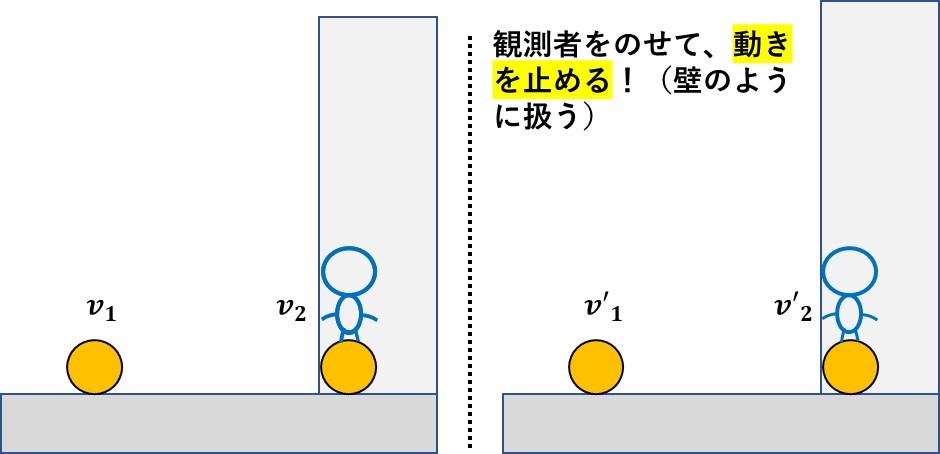
と、描くことができます!
この図を見ながら、『衝突後の速度は、衝突前と向きが逆で、大きさがe倍』の通りに式を作ると、
$${v_A}'-{v_B}'=-e(v_A-v_B)$$(後の速度は、前の速度と向きが逆でe倍)
となる。

あ!確かに覚えていた$$e=-\frac{{v_A}'-{v_B}'}{v_A-v_B}$$になっています!
これでわかってくれたかな?つまり、はね返り係数の公式は、下のように考えてあげればいいんだ!

はね返り係数の公式のまとめ
1.はね返ると、『衝突後の速度は、衝突前と向きが逆で、大きさがe倍』
2.2つの物体が動くときには、『衝突後の相対速度は、衝突前の相対速度と向きが逆で、大きさがe倍』で考える
【補足】跳ね返り係数eとエネルギー保存の関係
実は、はね返り係数の値によって、力学的エネルギー保存則が成り立つかどうかわかります!
問題を解くうえで、ヒントにもなりますから、頭の中に入れておきましょう。
| はね返り係数eの値 | 衝突の名前 | 力学的エネルギー保存則の成立 |
| e=1 | 弾性衝突 | 〇 |
| 0<e<1 | 非弾性衝突 | ✕ |
| e=0 | 完全非弾性衝突 | ✕ |
つまり、弾性衝突(e=1)のときは、力学的エネルギー保存則が使えるので、問題文を見た瞬間に、解法がぱっと思いつくようにしておきましょう!
まとめ:跳ね返り係数は分数で考えなければ簡単!
今回は、はね返り係数について紹介してきました!
この記事を読んで、『はね返りの式が上手く立てられない』なんてことはなくなったのではないでしょうか。
はね返りの問題を解くときには、『衝突後の速度は、衝突前と向きが逆で、大きさがe倍』を意識して解いてみてください!
今回は以上です。
関連記事運動方程式をあなたは本当に理解できてる??運動方程式を理解して力学の点数を爆上げする


