力のモーメントの計算問題を攻略！【公式＆解き方をわかりやすく解説】

悩んでる人

・力のモーメントって何？
・どんな公式で表されるの？
・どういう時に式を立てればいいの？

今回は、そんな受験生の悩みを解決していきます！

そして、最後には以下の例題を通して、モーメントの問題を解けるようにしていきますよ。

力のモーメントとは回転の大きさを表す

力のモーメントとは、物体を回転させる作用のことで、簡単に言えば、回転の大きさのことを表します。

悩んでる人

あまり想像ができないのですが、、

例えば、ドアを押して開ける時、なるべくドアのつけ根から遠いところを押した方が、楽に開けられるよね！あれは、力のモーメントが関係しているからなんだ！

塾長

つまり、物体を回転させる大きさは、力の大きさだけではなく、力を加える場所も大切だということになります。

なので、力のモーメントは、以下のようにあらわすことができます。

力のモーメントの公式

力のモーメントN
=力\(f\)×支点から力Fの作用線までの距離\(l\)

実際に問題を解くときには、

の順番で作図するようにしましょう！

例題：力のモーメントの計算問題

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

それでは一緒に解いていきましょう！

塾長

力のモーメントの計算問題の解き方

B端から重心までの距離を\(x\)とします。問題文をみると、水平面に物体が置かれているので、『物体が静止している』ことがわかります。

そして、A端B端それぞれをばねで持ち上げた時の状況が書かれているので、まずはその2つの状況を絵にかいてから、つり合いの式とモーメントの式を立てていきます。

その①：A端を持ち上げた時

力の図を描くと上のようになりますので、力のつり合いの式は、

$$ks+N_B=W・・・➀$$

となります。

次は、力のモーメントの式を立てていきましょう！

悩んでる人

あのー、支点ってどこにとればいいんですか？

いい質問だね！モーメントの支点は、多くの力が働いているところ、あるいは未知の文字があるところにとりましょう！

塾長

このように支点をとる理由は、支点に働く力は、うでの長さ\(l\)が0になるため、計算が楽になるからです！

今回は、垂直抗力\(N_B\)は自分で置いた文字、つまり未知数なので、B端をモーメントの支点にとると、モーメントの式は

$$ks×l=Wx・・・➁$$

となりますね！

今立てた式だけだと答えがわからないので、同様にB端を持ち上げた時のつり合いの式とモーメントの式を書いていきます。

その②：B端を持ち上げた時

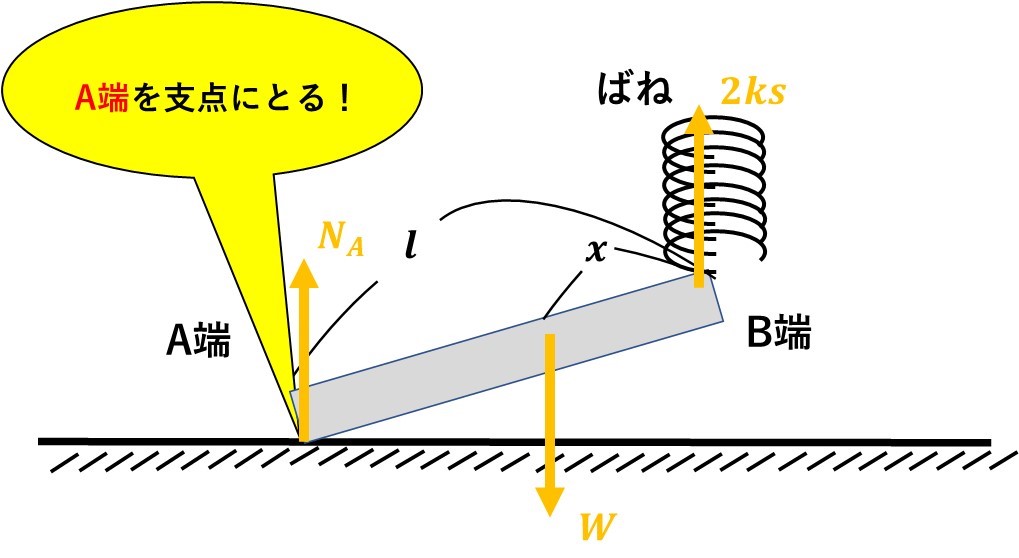
力の図を描くと上のようになりますので、力のつり合いの式は、

$$2ks+N_A=W・・・➂$$

となります。

次は、力のモーメントの式を立てていきます。

今回は、A端に働く垂直抗力を自分で\(N_A\)と置いたので、未知数があるA端をモーメントの支点として考えます。

A端をモーメントの支点とした時の、モーメントの式は、

$$W(l-x)=l×2ks・・・➃$$

力のつり合いと、力のモーメントの式は、以下のように求められました。

$$ks+N_B=W・・・➀$$
$$ks×l=Wx・・・➁$$
$$2ks+N_A=W・・・➂$$
$$W(l-x)=l×2ks・・・➃$$

今回知りたいのは、ばねの伸び\(s\)とB端から重心までの距離\(x\)なので、\(x\)と\(s\)が入っている➁と➃の式、つまり力のモーメントの式2本を連立すればわかり、答えは

$$s=\frac{W}{3k}$$$$x=\frac{l}{3}$$

となります。

今回は、つり合いの式はいらなかったってことだね！逆に言えば、モーメントの式を立ててなかったら解けなかったということなので、しっかり式を立てられるようにしておこう！

塾長

まとめ：まずは力のつりあいを考えてから力のモーメントの式を立てる！

今回は、力のモーメントについて詳しく話してきました。

力のモーメントの問題で、気を付けるべきことをまとめておきます！

上のことに気を付けながら、自分の持っている問題集で練習してみてくださいね！