今回は、こんな例題を解いていくよ!

例題
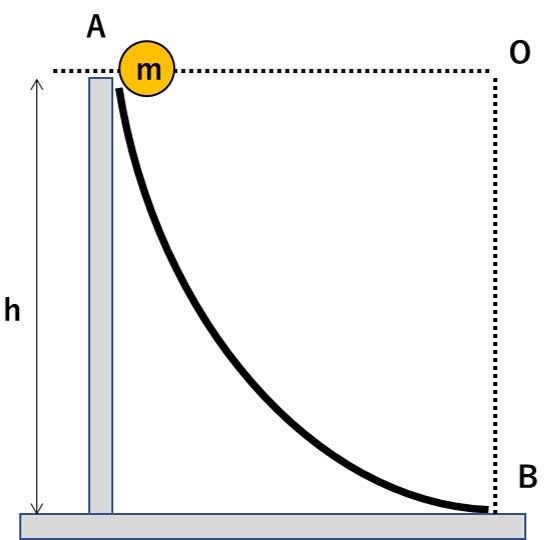
図の曲面ABは水平な中心Oをもつ半径hの円筒の鉛直断面の一部であり、なめらかである。曲面は点Bで床に接している。重力加速度の大きさをgとする。点Aから質量mの小物体を静かに放したところ、物体は曲面を滑り落ちて点Bに達した。この時の速さはいくらか。

この問題は、力学的エネルギー保存則を使って解けます!
正解!じゃあなんで、力学的エネルギー保存則が使えるの?


それは・・・
だから、物理の偏差値が上がらないんだよ(笑)

上の人のように、『問題は解けるけど点数が上がらない』と悩んでいる人は、使う公式を暗記してしまっているせいです。
そこで今回は、『どうしてこの問題では力学的エネルギー保存則が使えるのか』について説明していきます!
参考書にもなかなか書いていないので、この記事を読めば、周りと差がつけられますよ!
目次
力学的エネルギー保存則が使えると条件とは?

先に結論から言うと、力学的エネルギー保存則が使える条件は、以下の2つのときです!
力学的エネルギー保存則が使える時
1.保存力(重力、静電気力、万有引力、弾性力)のみが仕事をするとき
2.非保存力が働いているが、それらが仕事をしないとき
そもそも『保存力って何?』という方は、【保存力と非保存力の違い、あなたは知っていますか?意外と知らない言葉の定義を解説!】をご覧ください!
それでは、どうしてこのときに力学的エネルギー保存則が使えるのか、導出してみましょう!
導出【力学的エネルギー保存則の証明】
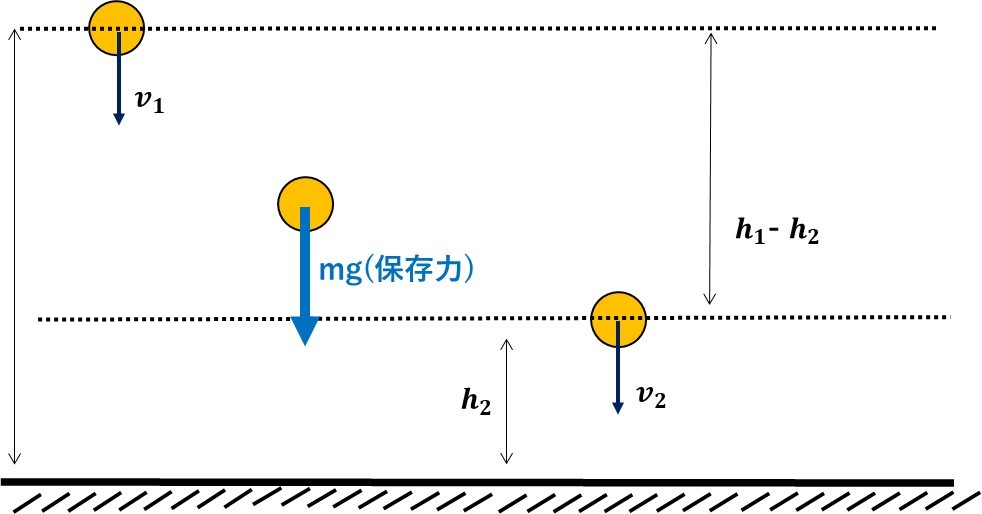
位置エネルギーの基準を地面にとり、質量mの物体を高さ\(h_1\)から\(h_2\)まで落下させたときのエネルギー変化を見ていきます!
保存力と非保存力の違いでどうなるか調べるために、まずは重力のみで考えてみよう!

その①:物体に重力のみがかかる場合
それでは、エネルギーと仕事の関係の式を使って導出していくよ!

エネルギーと仕事の関係の式って何?という人は、【エネルギーと仕事の関係をあなたは導出できますか?物理の問題を解くうえでどういう時に使うべきかについて徹底解説!】をご覧ください!
エネルギーと仕事の関係
$$\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2=Fx$$
エネルギーの仕事の関係の式は、『運動エネルギー』は『仕事(力がどれだけの距離かかっていたか)』によって変化するという式でした!
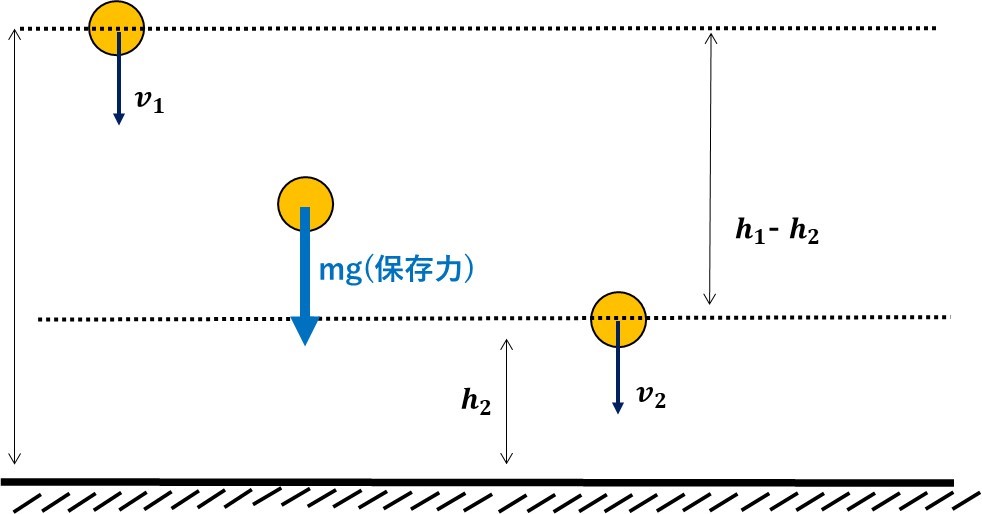
図を見ると、重力のみが\(h_1-h_2\)の間で仕事をしているので、エネルギーと仕事の関係の式は、
$$\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2=mg(h_1-h_2)$$
となります。移項して、
$$\frac{1}{2}m{v_1}^2+mgh_1=\frac{1}{2}m{v_2}^2+mgh_2$$(力学的エネルギー保存)
となります。
つまり、保存力(重力)の仕事では、力学的エネルギーは変化しないということがわかりました!
その②:物体に保存力+非保存力がかかる場合
次は、重力のほかにも、非保存力を加えて、エネルギー変化を見ていきましょう!
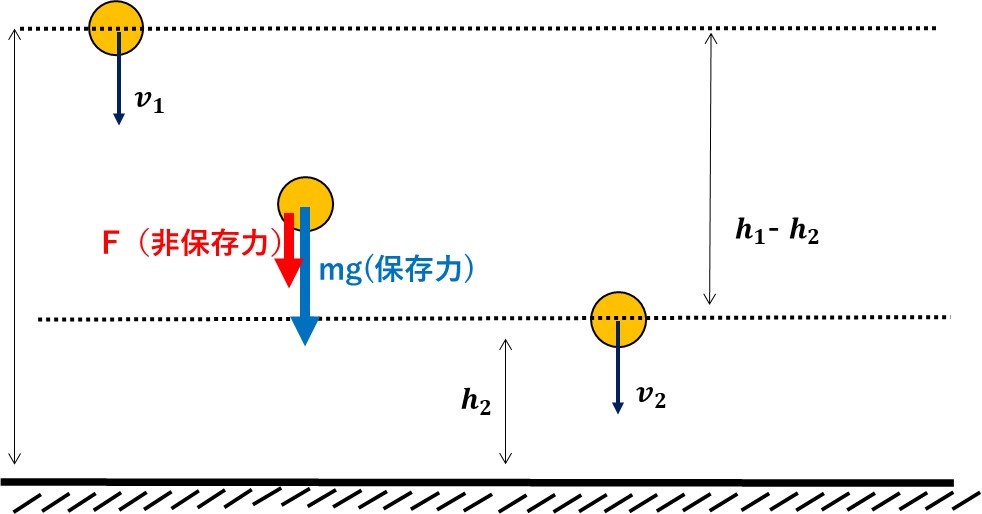
さっきの状況に加えて、\(h_1-h_2\)の間で非保存力Fが仕事をするので、エネルギーと仕事の関係の式から、
$$\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2=mg(h_1-h_2)+F(h_1-h_2)$$
$$(\frac{1}{2}m{v_1}^2+mgh_1)-(\frac{1}{2}m{v_2}^2+mgh_2)=F(h_1-h_2)$$
上の式をみると、非保存力の仕事では、その分だけ力学的エネルギーが変化していることがわかります!
つまり、非保存力の仕事が0であれば、力学的エネルギーが保存するということができました!
力学的エネルギー保存則が使える時
1.保存力(重力、静電気力、万有引力、弾性力)のみが仕事をするとき
2.非保存力が働いているが、それらが仕事をしない(力の方向に移動しない)とき

なるほど!だから上のときには、力学的エネルギーが保存するんですね!
理解してくれたかな?それでは問題の解説に行こうか!

問題の解説:力学的エネルギー保存則
例題

図の曲面ABは水平な中心Oをもつ半径hの円筒の鉛直断面の一部であり、なめらかである。曲面は点Bで床に接している。重力加速度の大きさをgとする。点Aから質量mの小物体を静かに放したところ、物体は曲面を滑り落ちて点Bに達した。この時の速さはいくらか。
考え方
物体にかかる力は一定だが、力の方向は同じではないので、加速度は一定にならず、等加速度運動の式は使えない。2点間の距離が与えられており、保存力のみが仕事をするので、力学的エネルギー保存の法則を使う。
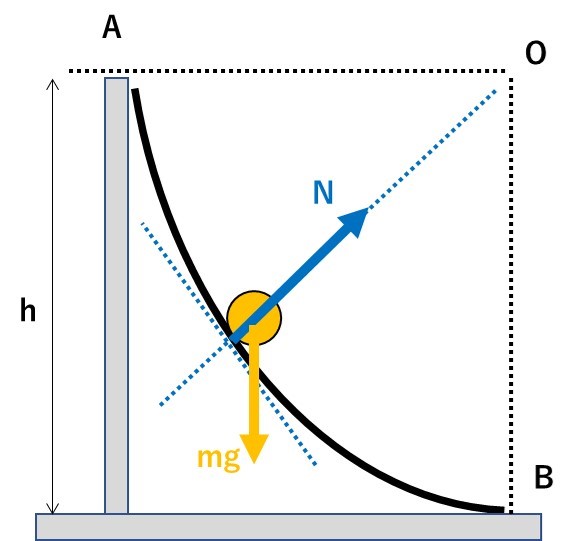

あれ?非保存力の垂直抗力がありますけど・・
実は垂直抗力は、常に点Oの方向を向いていて、物体は曲面接線方向に移動するから、力の方向に仕事はしないんだ!


これが、『2.非保存力が働いているが、それらが仕事をしない(力の方向に移動しない)とき』ですね!
なので、普通に力学的エネルギー保存の法則を使うと、
$$0+mgh+0=\frac{1}{2}mv^2+0+0$$(運動エネルギー+位置エネルギー+弾性エネルギー)
$$v=\sqrt{2gh}$$
となります。
まとめ:力学的エネルギー保存則は必ず証明できるようにしておこう!
今回は、『どういう時に、力学的エネルギー保存則が使えるのか』について説明しました!
力学的エネルギー保存則が使える時
1.保存力(重力、静電気力、万有引力、弾性力)のみが仕事をするとき
2.非保存力が働いているが、それらが仕事をしない(力の方向に移動しない)とき
これら2つのときには、力学的エネルギー保存の法則が使えるので、しっかりと覚えておきましょう!
くれぐれも、『この問題はこうやって解く!』など、解法を問題ごとに暗記しないでくださいね。


