
単振動苦手なんです・・・
力学の範囲ももう少しで終わりますが、単振動あたりから苦手な人が増えてきます。
確かに、バネやら周期やらいろいろ出てきて、混乱してしまいますよね!
しかし苦手になる人の共通点として、『単振動の公式を丸暗記している』ということです。
そこで今回は、苦手な人が多い単振動について紹介していきます。
この記事を読めば、受験生の中でも差がつくので、しっかり勉強していきましょう!
目次
【公式】単振動は等速円運動を射影したもの

単振動は、等速円運動を横から見た時の、往復運動のことをいいます。
つまり、単振動と円運動は密接につながっているのです!
ばねの単振動が有名だけど、時計の振り子とかも単振動だよ!

等速円運動と単振動を比較
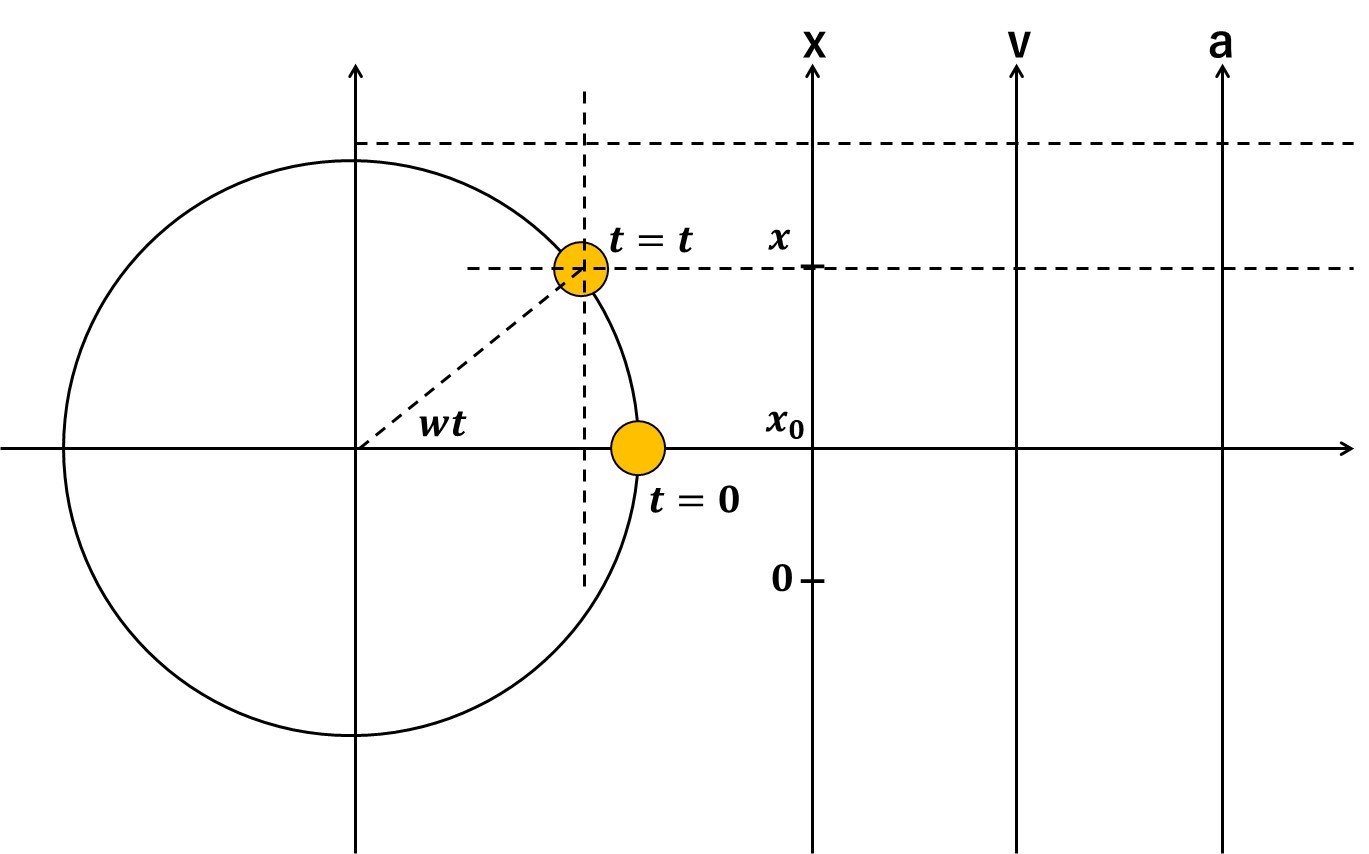
ここからは、単振動の加速度を導出していきますので、紙とペンを用意して、実際に描いてみましょう!


上の図の描き方
➀半径A、角速度wtの円運動を、t=0,t=tの2つ描く。
➁円の隣に、紙面上方向を正方向にとった3本の軸を描く。
➂図のように、文字を描きこむ。
ここまで描けましたか?描けたら、単振動における\(x,v,a\)を導いていきます。
数Ⅲをやっている人なら、微分すれば簡単に導出できますが、今回は数Ⅲをやっていない人でもできる方法で、導出していきます。
※この導出は物理のエッセンスにも載っていないので、予備校に通っている人と差がつきます!物理で点数を取りたければ、導出を侮るなかれ。
【公式の証明】単振動の位置\(x\)の導出
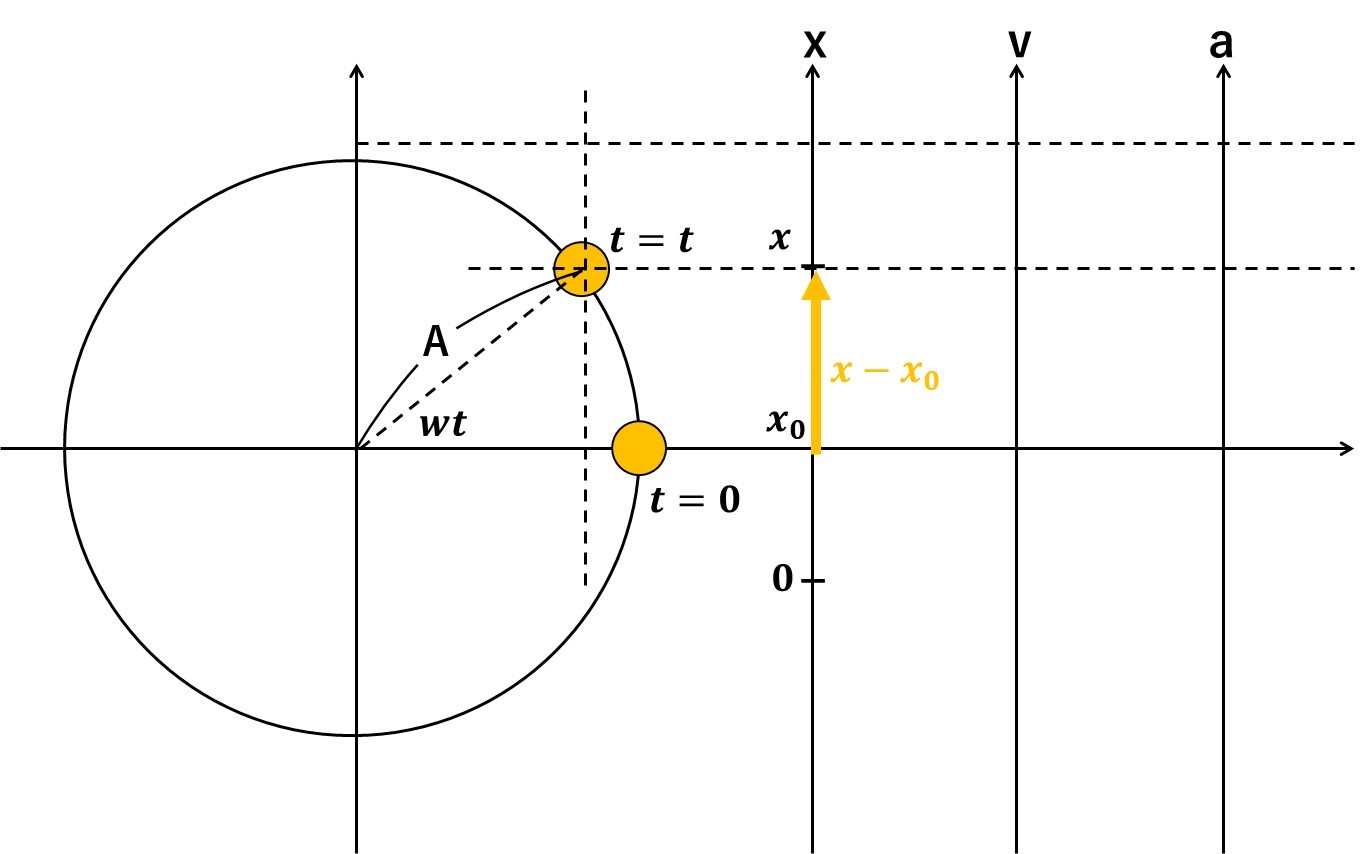
まずは、オレンジの矢印\(x-x_0\)の長さを求めていきます。
円の中にある三角形に着目すると、三角形の縦と\(x-x_0\)の長さが等しいことがわかります。
三角形の中で、\(sinwt\)を求めると、
$$sinwt=\frac{x-x_0}{A}$$となるから、$$x-x_0=Asinwt$$となり、単振動の変位が求まりました。
【公式の証明】単振動の速度\(v\)の導出
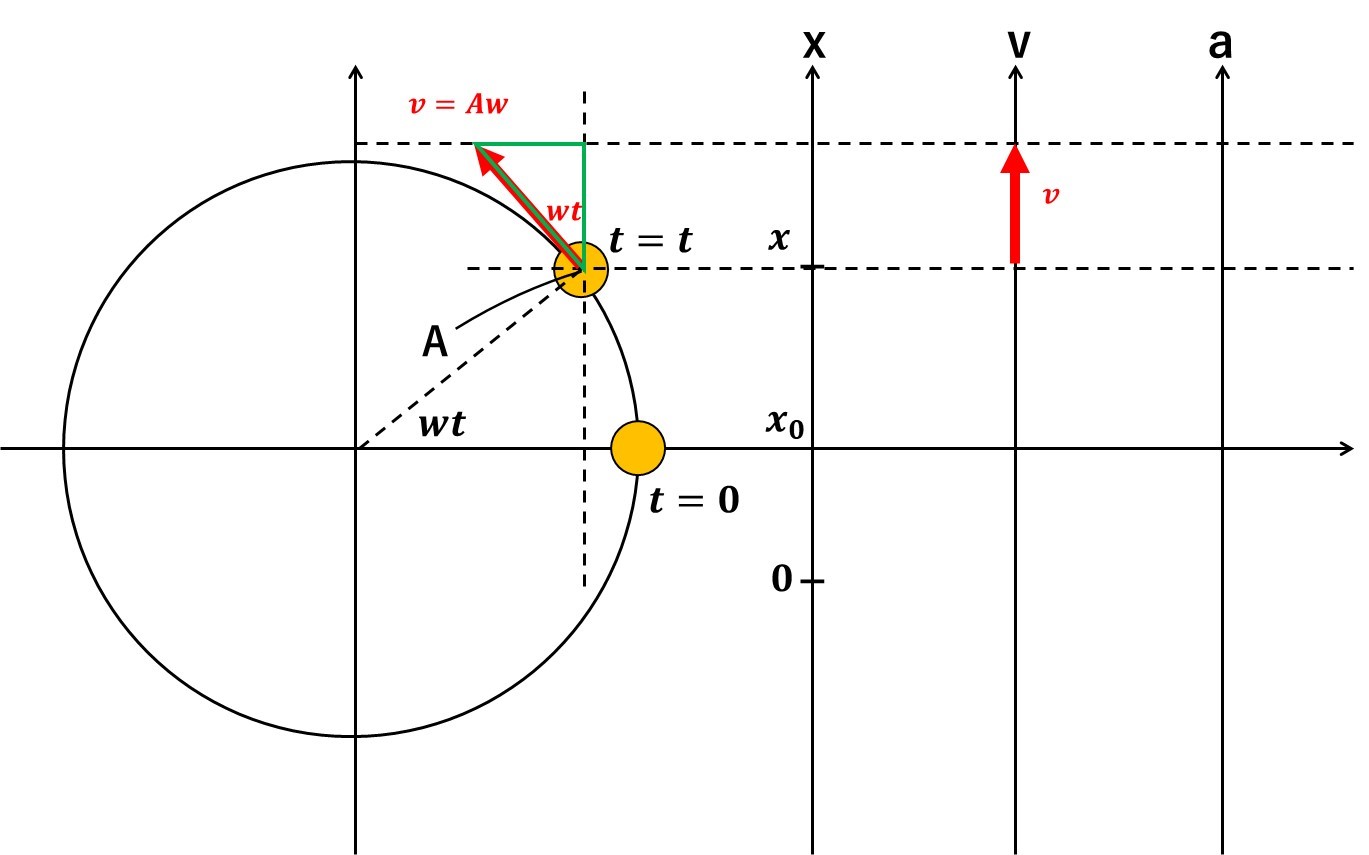
続いて、\(v\)軸上の赤矢印の部分、単振動の速度\(v\)を求めていきます。
円運動の速度は、接線方向(円から伸びる赤矢印)に生じ、その大きさは、
$$w=\frac{v}{r}$$$$v=rw$$と求められました。今回、半径がAであるので、円運動の速さは、図のように
$$v=Aw$$となります。

次は、円内の緑色の三角形に着目すると、\(v\)軸上の赤矢印の部分の長さは、
$$v=Awcoswt$$
と求めることができます!
【公式の証明】単振動の加速度\(a\)の導出
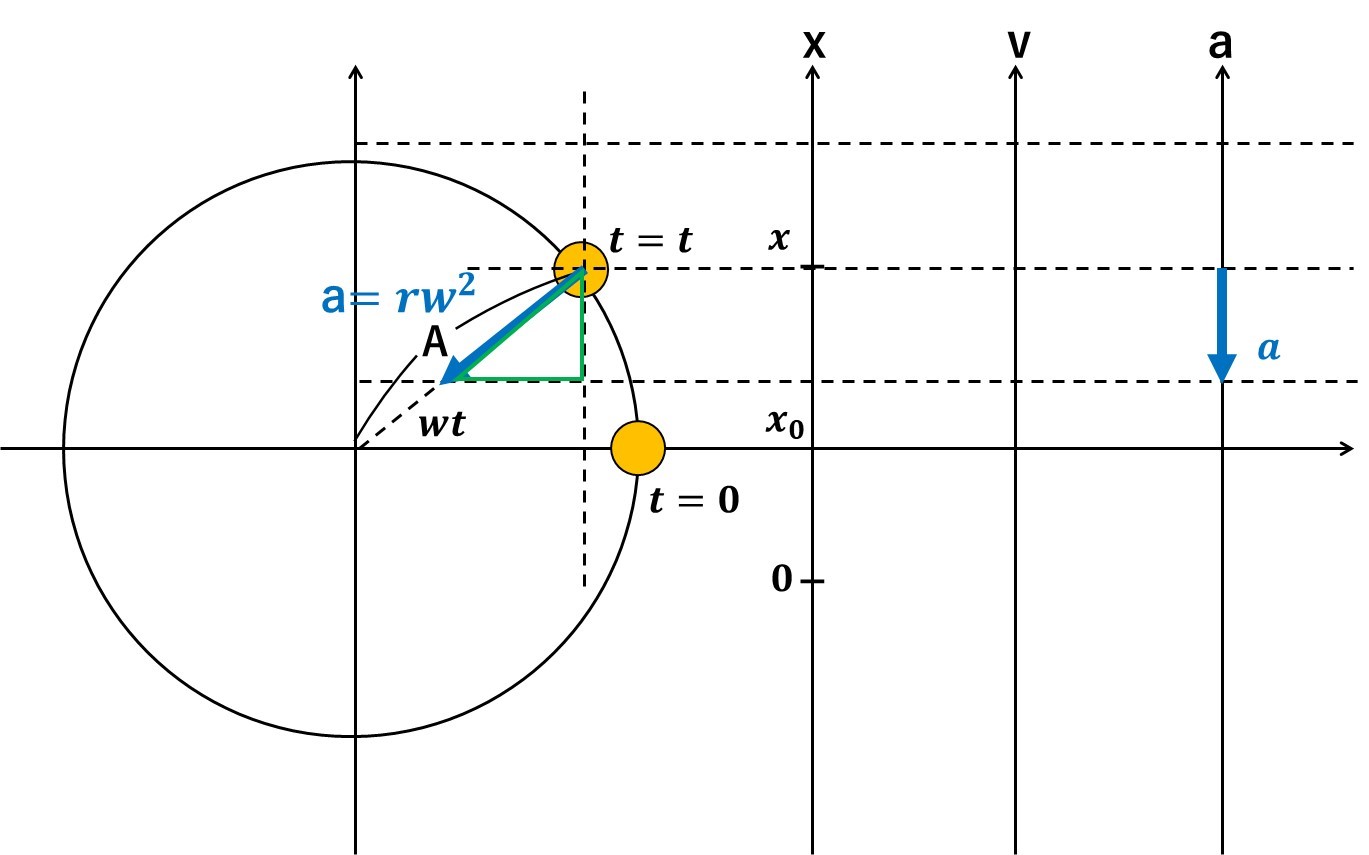
最後に、\(a\)軸上の単振動の加速度を求めていきます!
あともう少しだから、一緒に頑張ろう!

等速円運動において、加速度は中心方向に$$a=rw^2$$と働くのでした。
今回、円の半径はAなので、等速円運動の加速度の大きさは、$$a=Aw^2$$
となります。

\(a\)軸上の単振動の加速度の青矢印の長さは、円内にある緑色の三角形の辺と同じだから、
$$a=-Aw^2sinwtとなります$$
また、位置\(x\)の導出で求めた \(x-x_0=Asinwt\)を代入すると、
$$a=-w^2(x-x_0)$$
となります!

どうして、加速度がマイナスなのですか?

図を見てごらん。単振動の加速度の矢印は、最初にとった軸の正方向とは、逆向きになってるよ!


なるほど!軸とは逆向きだから、マイナスがつくのですね!
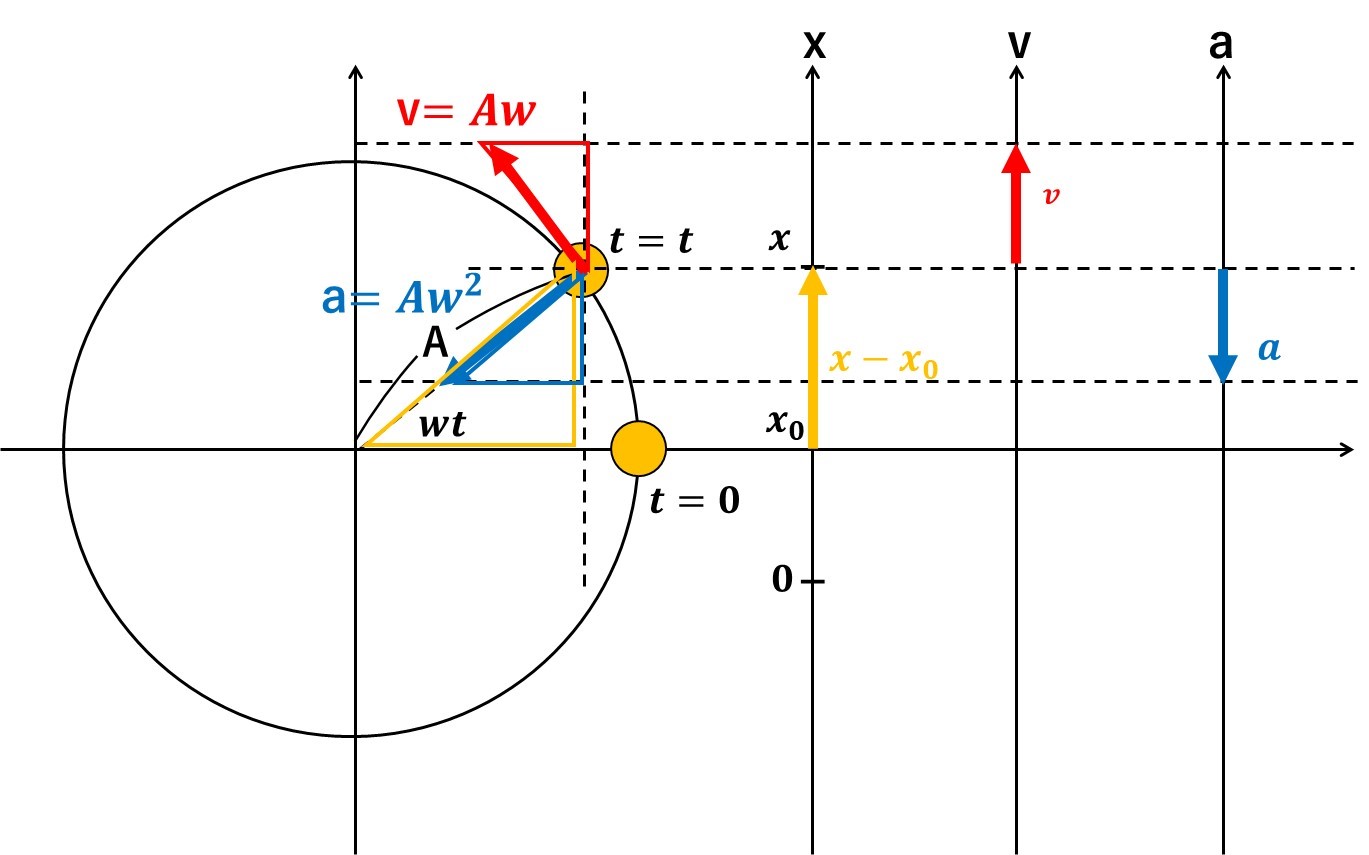
一応、3つの関係がどうなっているのか、上の図にまとめてみました。
そして、単振動の加速度は\(角振動数をw、振動中心をx_0\)とした時、
$$a=-w^2(x-x_0)$$
と表せることが、導けましたね!
単振動の加速度
単振動の加速度は、\(角振動数をw、振動中心をx_0\)とした時、
$$a=-w^2(x-x_0)$$
まとめ:単振動の公式は微分で求めてもOKです

今回は、単振動の加速度を、微分を使わずに図形的に求めてみました。
今回の導出のやり方がわからない人は、数学Ⅰの範囲の図形の範囲の理解が、まだ浅い可能性がありますので、よく復習しておきましょう!
また、数Ⅲを習っている人は、単振動の位置をtで微分していくと加速度を導出できますので、ぜひやってみてください。
そして、単振動の問題を解くには、以下の2点に気を付ける必要があります!
単振動のポイント
➀まず、任意の位置\(x\)における運動方程式を立てる!
➁必ず\(x\)軸と同じ向きに加速度の正方向をとる!

どうして、必ず\(x\)軸と同じ向きに加速度の正方向をとらなくちゃいけないのですか?
ちゃんと導出した人なら分かるはずなんだけれどなあ



あ!導出のときに\(x\)軸と同じ向きに加速度の正方向も同じ向きに決めたからですね!
正解!これは独学だと見落としやすいから、しっかり覚えておこう!

次の記事では、実際に単振動の問題を解いていきます。


