
・円運動の向心加速度って何?
・角速度って何?
・公式の導出ってどうやるの?
今回は、そんな悩みについて解決していきます!
円運動といえば、思いつくのが、
$$v=rw$$$$a_向=rw^2=\frac{v^2}{r}$$
の2つかと思いますが、この2つの公式を導くことってできますか?
もし、導くことができないようであれば、この先物理の成績が伸びないと断言できます!
そうならないためにも、導けない人は、しっかりと導けるようにしましょう。
✔この記事の内容
・円運動における向心加速度
・公式の導出
・角速度や周期の言葉の意味
向心加速度は円運動の向きを変える!


加速度って速さを変えるものでは?
確かにそうだね!けれど加速度はベクトルだから『向き』も持つよね!

等速円運動では、常に中心方向に対して力が働いているため、加速度を持ちます。(運動方程式をみれば力がかかれば加速度が生じるのは明らか)
この加速度のことを、向心加速度といい、円運動の速さには関係しない加速度になります。
ココがポイント
・力は常に\(v\)と直交するため、速さは変わらない
・しかし、中心方向に加速度(向心加速度)が働くので、\(v\)の向きは変わる
円運動の公式の導出【物理の理解を深める!】
$$v=rw・・・➀$$
$$a_向=rw^2=\frac{v^2}{r}・・・➁$$
の二つの公式を導いていこう!
➀の場合
導出の前に、円運動で使われる言葉の意味を2つ、知っておこう!
周期\(T\)[s]:1回転するのにかかる時間
角速度\(w\)[rad/s]:1秒当たりに回転する角度
円運動は『円』なので、半径がrの円なら一回転すれば、角度は2\(\pi\)だし、道のりは2\(\pi r\)ですね!
つまり、周期(1回転するのにかかる時間)を使って
$$wT=2\pi ・・・➀$$$$vT=2\pi r ・・・➁$$
と書くことができます。
上の式もとても大切なので、しっかり理解しておきましょう!
➁÷➀をすると、
$$\frac{vT}{wT}=\frac{2\pi r}{2\pi}$$$$\therefore v=rw$$
となり、1つ目の公式を導くことができました!

周期や角速度などの、言葉の意味を理解しておくことが大切なのですね!
➁の導出
公式の導出の前に、扇形の弧の公式について確認しておこう!

中学生でも360°を使って習った公式だから、忘れていた人は思い出しておこう!

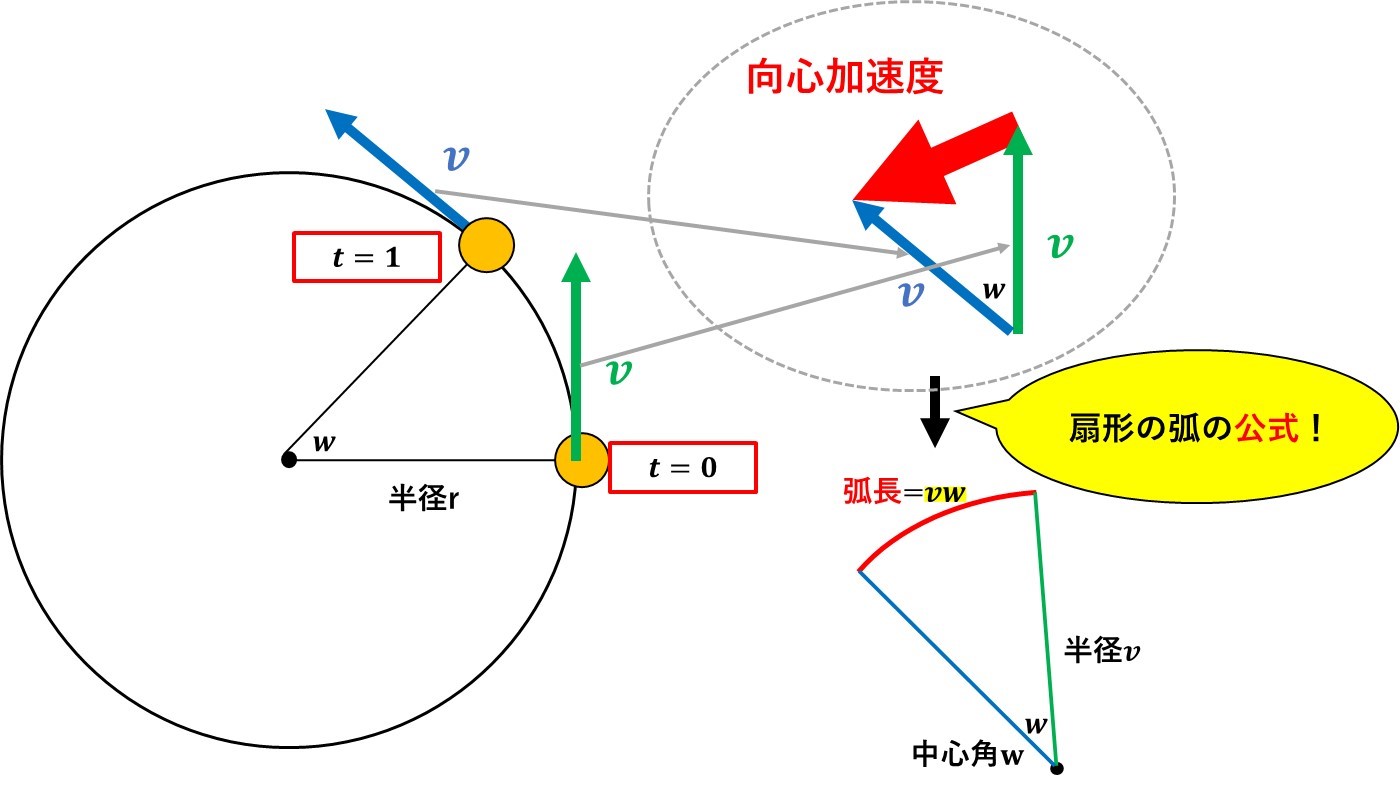
加速度は、『1秒間当たりの速度変化』なので、上の図のように\(t=0\)と\(t=1\)の速度ベクトルの差をとれば加速度がわかります!
扇形の公式を使って、加速度ベクトルを求めると、
$$a_向=vw$$
と求めることができます。
これに、➀の導出で求めた
$$v=rw$$
を代入すると、
$$a_向=vw=rw^2=\frac{v^2}{r}$$
となり、公式を導出できました。
こんな感じで、しっかり公式を導出できるようにしておこう!

まとめ:円運動の公式を導出できるようにしておこう!

今回は、円運動の公式の導出について話してきました。
$$v=rw・・・➀$$
$$a_向=rw^2=\frac{v^2}{r}・・・➁$$
上の公式は、丸暗記しないでしっかりと求められるようにしておくことが大切です!
また、周期や角速度などの言葉の意味を覚えておくことで、公式への理解も深まりますよ。

