
・複雑な回路問題になると、どこから解いたらいいかわからない!
こんな悩みを解決していきます。
実は、電磁気の回路問題は、『やり方を覚えれば』物理の科目の中で、最も安定して得点することができます。
今回は、そんな回路問題の必勝法について、丁寧に説明していきます。
記事の最後には、例題もありますので紙とペンを用意して、しっかり手を動かしてやってみましょう!
前回の記事は導体と誘電体の違いとは?【誘電体を挿入するとコンデンサーの容量が増える理由】を参考にどうぞ。
目次
【まずは押さえる!】回路問題を解くための作図のルール
まずは問題を解くための、作図の仕方について紹介します!
この作図を必ずやることが、回路問題を正確に解くコツにもなりますので、しっかりと覚えておきましょう。
作図のポイント
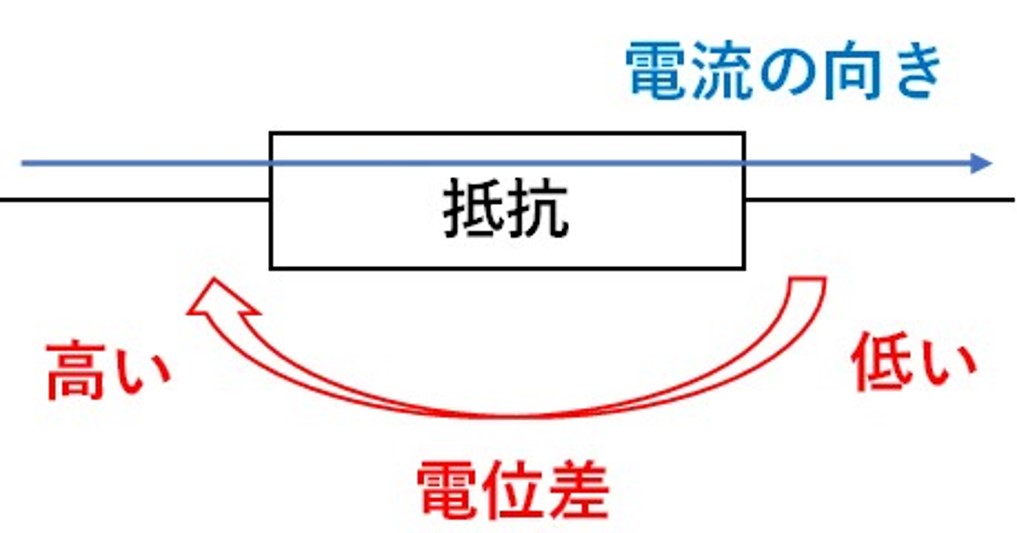
・電流の流れを矢印を使って書く!
・電圧は高い方(高電位の方)を矢印の先端にして書く!
1.電流

電流とは、簡単に説明すると、『電子の流れ』のことです。
電流は、よく『水の流れ』に例えられ、水と同じように電流も、高いところから低い方へと流れていきます。

つまり、電位差(回路の高低)がわかれば、自動的に電流の流れる方向がわかってしまうのです!
このサイトでは、電流の流れを『青矢印』で書いていますので、自分でもしっかり描けるようにしましょうね!
電位(電位差)
回路内は、電池などの装置によって、電気的な高低差が生じています。
この電気的な高さのことを、『電位』と呼び、高さの差のことを『電位差』といいます!

電位の差のことを、電位差というので間違えないように注意!
このサイトでは、電位差を高い方の電位を先端にして、『赤矢印』で作図していくので、皆さんも作図していってください!
つまり、矢印を作図することで、矢印の先端が高電位だということがわかるのです!
この2つのルールをもとにして、回路問題を解いていきます。
【高校物理】電磁気回路問題の解き方を解説
それでは、回路問題の解き方について説明していきます!
回路問題の解き方は、以下の3ステップのみで完結します。
回路問題の解法
1.電荷・電流を置く!(あるいは電位差を置く)
2.抵抗・コンデンサーの電位差を書き込む!
3.回路方程式を立てて1.を求める!
必ずどの問題も、この手順で解けますので、例題とともに一緒に見ていきましょう!
【例題】
スイッチを閉じて十分時間後のC1,C2に溜まっている電荷を答えよ。
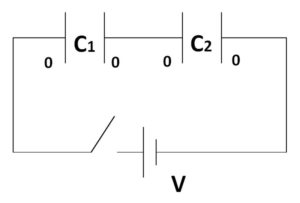
1.電荷・電流を置く!(あるいは電位差を置く)
まずは数学の文章題と同じように、求めたいものを文字で置くという作業をしましょう!
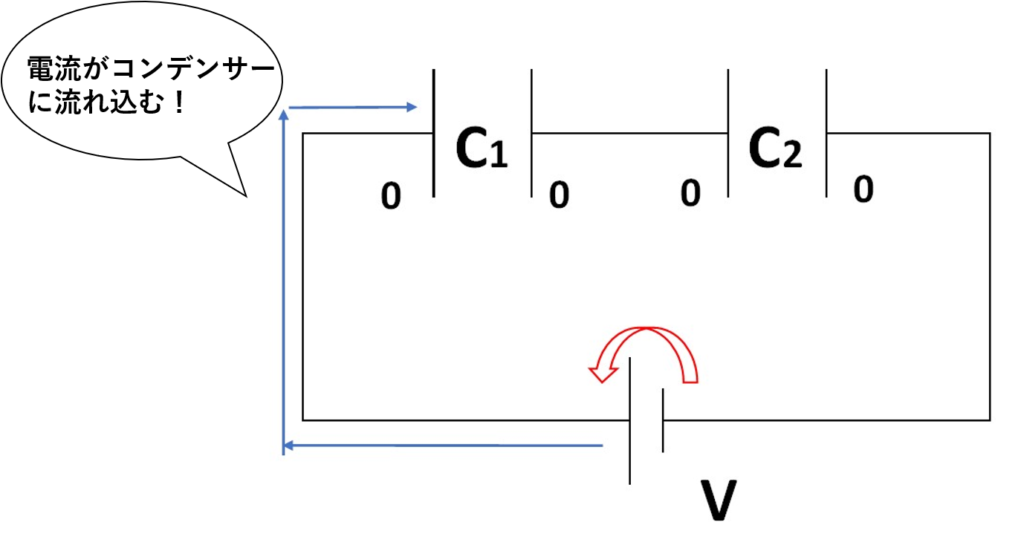
スイッチをつなぐとこんな感じで、電流がコンデンサーに流れ込み、コンデンサーに電荷が溜まります。
コンデンサーがあるので、今回は電流ではなくて『電荷』を置いていきましょう。
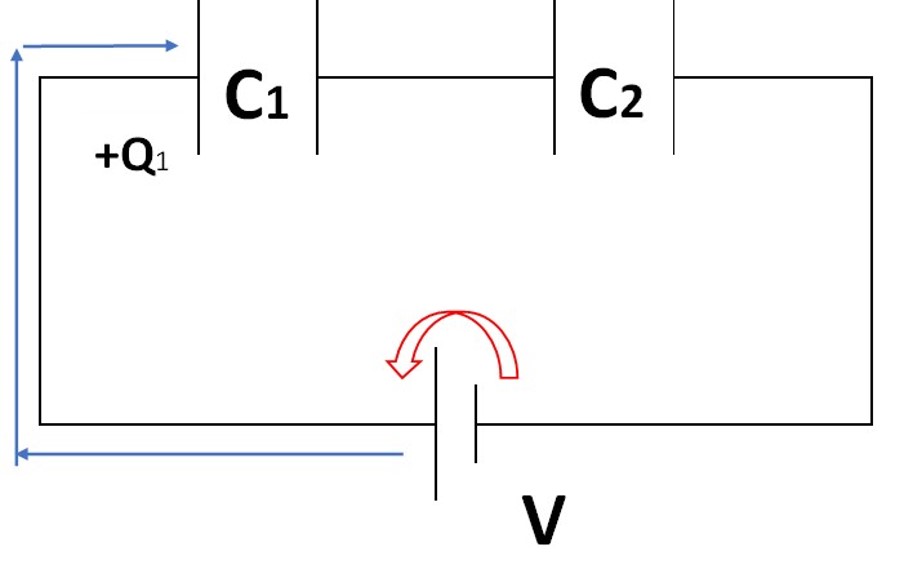
電流が流れ込んできた方のコンデンサーの方には、プラスの電荷が溜まります!
この電荷の大きさを、+Q1と自分で置きます。
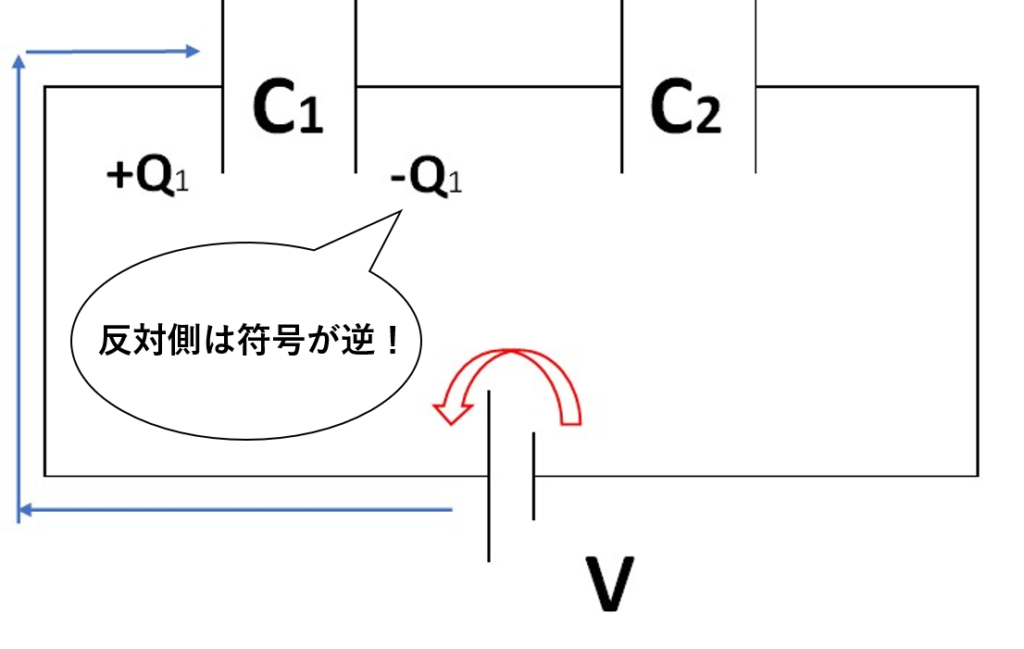
その時、反対側のコンデンサーには、符号が逆向きで大きさが同じ電荷が溜まります!
同じようにして、もう一つのコンデンサーも電荷を置きましょう。
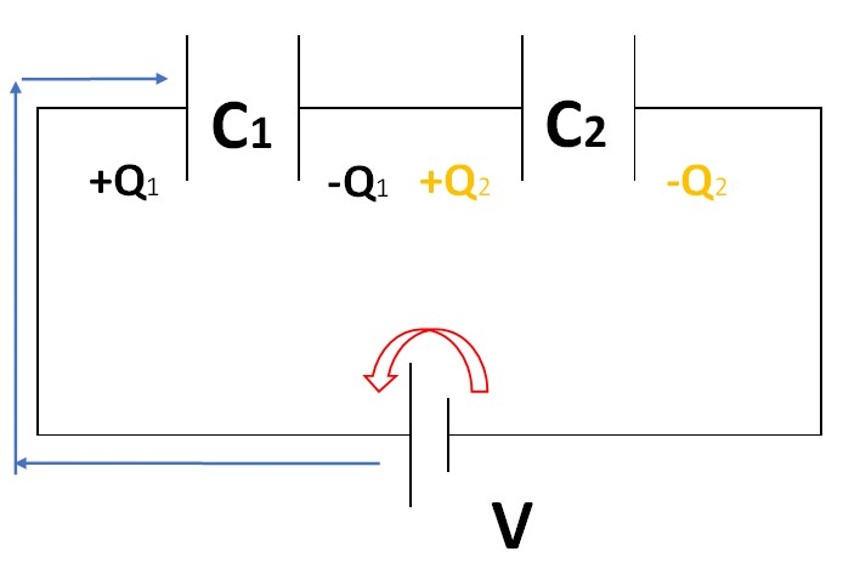
ここまで書けましたか?
次は、二番目の手順で、コンデンサーに電位差を書いていきます!
2.抵抗・コンデンサーの電位差を書き込む!
それでは、ステップ1で描いた図をもとに、コンデンサーに電位差を書いていきます!
コンデンサーにかかる電圧は、
$$V=\frac{Q}{C}$$
と表すことができますので、それぞれのコンデンサーにかかる電圧は、
$$V_1=\frac{Q_1}{C_1}$$
$$V_2=\frac{Q_2}{C_2}$$
と書くことができますね!
この時の電位の矢印の向きは、プラスの電荷が溜まっている方が、高電位になります。
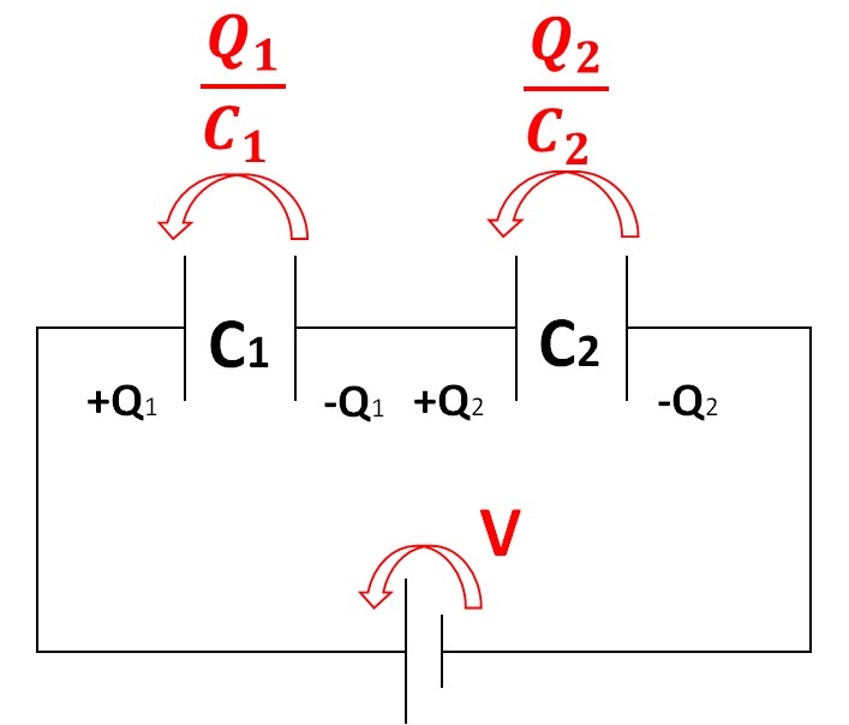
ここまで描けたら、最後は回路方程式を立てて終わりです。
残り1ステップ一緒に頑張っていきましょう!
3.回路方程式を立てて1.を求める!
さて、最後は回路方程式を立てていきます。
回路方程式
1.電荷保存・電流保存の式
2.任意のループ1周での電位の関係式(キルヒホッフの第二法則)
1.電荷保存・電流保存の式
まずは、コンデンサーがあるので、電荷保存の式を考えていきます。
電荷保存の式は、コンデンサーの島を見つけて、動作の前と後での電荷の変化を見て式を立てます。
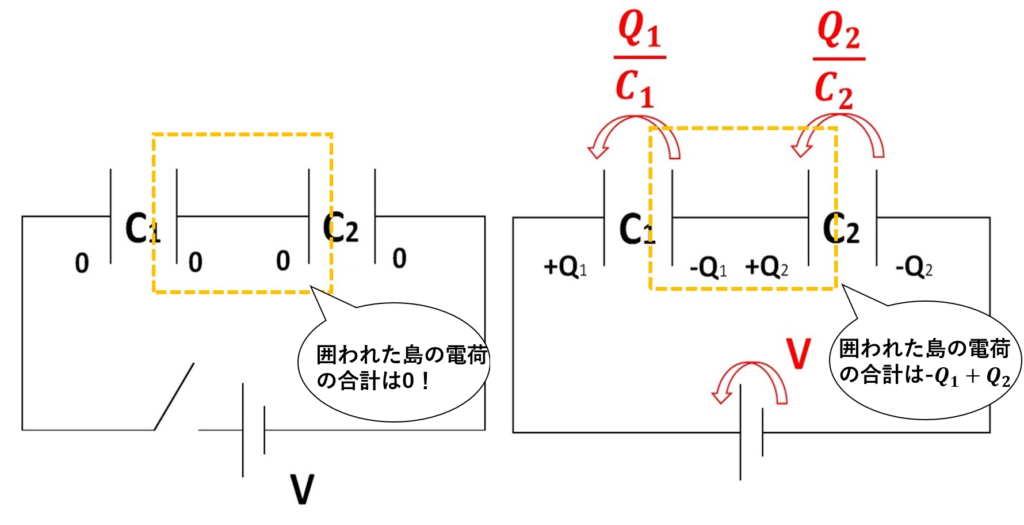
コンデンサーの島(オレンジで囲ったところ)の中では、電荷が動作前後で保存します。
よって、電荷保存の式は、
$$0+0=-Q_1+Q_2・・・➀$$
と書くことができます!
電荷保存の式を立てるためには、上のように『動作前後の図』が必要になりますので、図は必ず操作するごとに描くようにしましょう!
2.任意のループ1周での電位の関係式(キルヒホッフの第二法則)
回路は、任意のループで一周して同じ場所に戻ると、電位の変化は0になります!

ちょっとわかりづらいです、、
例えば、ショッピングモールに行ったとしましょう。

一階のある場所から、エスカレーターを使って2階3階と上がって、同じ場所に戻ってこようとしたら、必ず上った分だけエスカレーターで下がりますよね。
つまり、何階まで上ろうとも、同じ場所に戻ってきたら、高さの変化は0になります!

回路にも同じことが言えて、回路内での高さ変化は、赤矢印によって示されています!
回路を一周なぞったときに、矢印の根元から先端に向かってなぞれば上昇。
逆に、先端から根元に向かってなぞれば、高さは下降です!
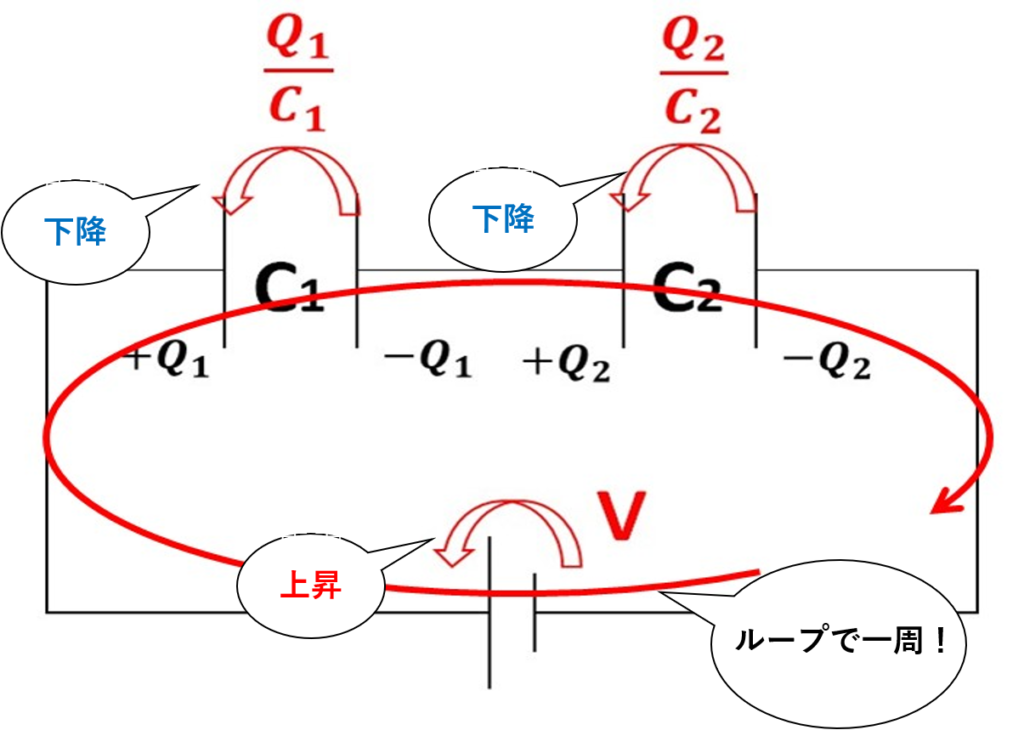
上の写真のように、任意の閉回路を一周したとき、電位は上昇と下降を繰り返して、同じ場所に戻ってきます。
上昇をプラス、下降をマイナスとして、式を立てると、
$$V=\frac{Q_1}{C_1}+\frac{Q_2}{C_2}・・・➁$$
となります!
➀と➁の式を連立して解くと、
$$0+0=-Q_1+Q_2・・・➀$$
$$V=\frac{Q_1}{C_1}+\frac{Q_2}{C_2}・・・➁$$
$$Q_1=Q_2=\frac{C_1C_2}{C_1+C_2}V・・・(答)$$
と解くことができます。
まとめ:電磁気の回路問題は確実に解けるようにしよう!

今回は、回路問題を解く方法について紹介してきました!
今回紹介した例題は、比較的簡単でしたので、簡単に解いてしまった方もいるかもしれませんが、解けるというよりもしっかりと解き方をマスターすることが、非常に重要です。
やり方をしっかりと覚えて、自分が持っている問題で回路問題を練習してみてください!
今回は以上です。
関連記事【高校物理】回路問題で立てる式はたった3本【回路方程式の解き方を解説】


