
・壁にはね返る、ドップラー効果の解き方がわかりません
・壁が動くと、なおさら難しく感じます
今回は、壁に反射するドップラー効果について話していきます。
センター試験や、私大入試でも出題されやすい範囲なので、しっかりできるようにしておきましょう。
✔この記事の内容
・ドップラー効果の解き方
・壁があるときの問題の解き方
✔この記事の信頼性
浪人時に苦手だった物理を、記述模試偏差値65以上、センター試験満点近くまで伸ばした『考え方』や『解き方』について、大切なエッセンスを『ぎゅっと』凝縮してまとめています。
目次
壁が動くドップラー効果の解き方は2ステップ!
壁が動くとき、あるいは動かないときの問題の解き方は、たった2ステップです。
解き方!
➁壁に音源を取り付け、➀の振動数を出していると考える!

なんか、簡単に解けそうですね!
解き方だけ見てもわからないと思うから、実際に例題をみて、確認してみよう!

例題:反射があるドップラー効果の問題の解き方
例題

移動できる鉛直な壁の前方に、振動数\(f_0\)の音源が静止しており、そのさらに前方に人がいる。今、壁が音源に向かって速さ\(u\)で近づくとき、音源から速さ\(v\)で遠ざかる人がその反射音を聞くと、いくらの振動数に聞こえるか。ただし、音速をVとする。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
手順➀:壁に観測者を置いて壁で観測する振動数を求める
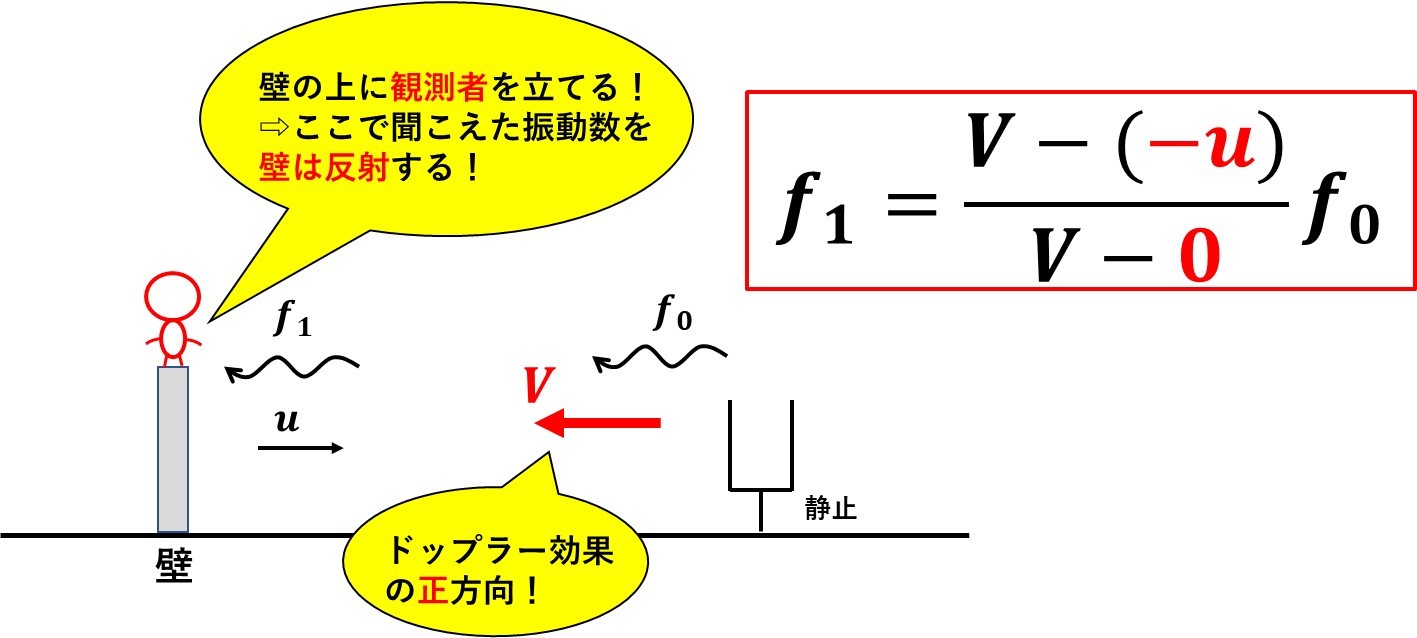
まずは、壁の上に観測者をおいて、その場所で聞こえる振動数を求めます!
ドップラー効果は、音源から観測者方向を正方向として、速度を代入するので、今回の場合は壁(観測者)の速度は、音速と向きが逆なので、マイナスで代入します。
符号に気を付けながら、ドップラー効果の式を用いて、壁で聞こえる振動数\(f_1\)を求めると、
$$f_1=\frac{V-(-u)}{V-0}・・・➀$$
となります。
あと、もう1ステップだけだよ!

手順➁:壁に音源を取り付けて➀の振動数を出していると考える
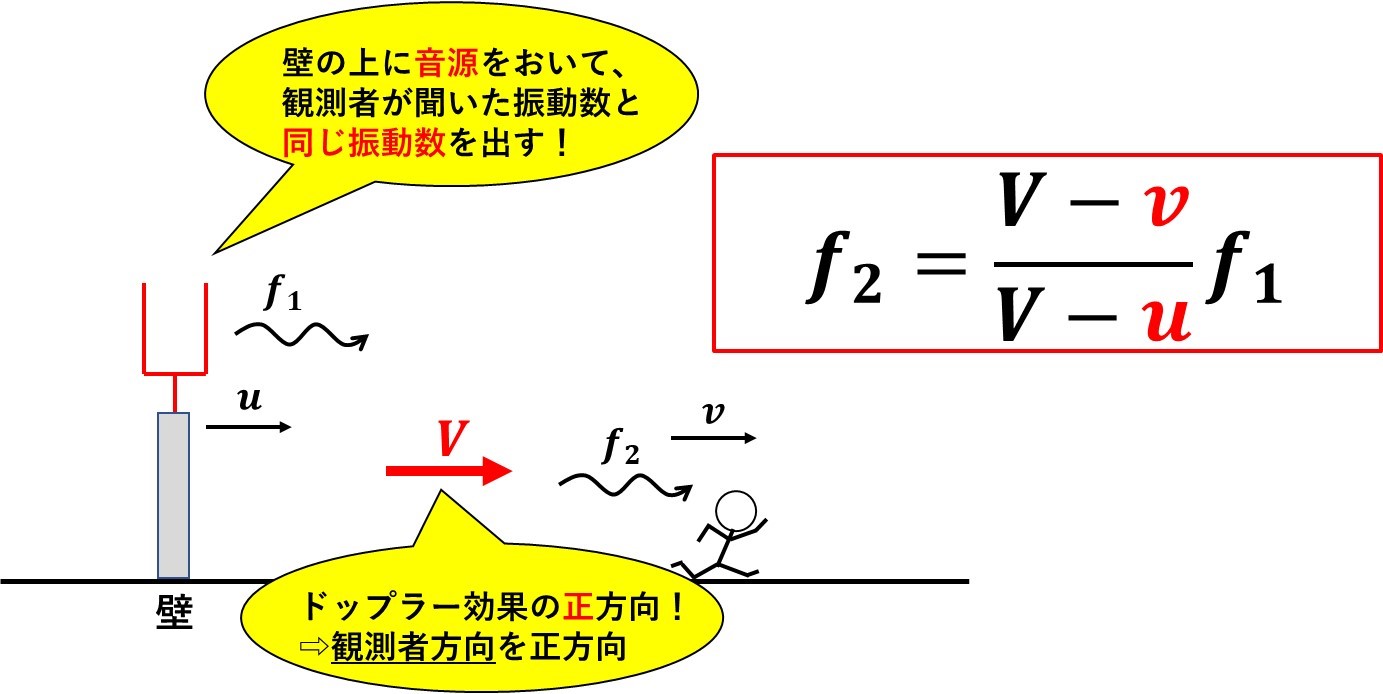
最後に、さっき観測者がいた壁の上に、観測者が聞いた振動数と、同じ振動数が出せる音源を置きます。
音源と、観測者の場所が変わったので、ドップラー効果の正方向も変化することに注意だよ!


右向きに走る観測者が聞く振動数\(f_2\)は、ドップラー効果より
$$f_2=\frac{V-v}{V-u}f_1・・・➁$$
となります。
➁に➀を代入して、
$$f_2=\frac{V-v}{V-u}f_1$$$$f_2=\frac{V-v}{V-u}×\frac{V-(-u)}{V-0}$$$$\frac{(V-v)(V+u)}{V(V-u)}・・・答え$$
となります。
要点を押さえれば、簡単だね!

まとめ:壁の反射があるドップラー効果問題

今回は、壁があるドップラー効果について話してきました。
壁が動くとき、あるいは動かないとき、どちらでも問題の解き方は、たった2ステップでした!
解き方!
➁壁に音源を取り付け、➀の振動数を出していると考える!
ドップラー効果の公式を覚えて、音速の方向を正方向にとり間違えなければ、間違うことはありませんね!
自分の持っている問題集でも、上の方法で解けるかどうか、確認してみましょう。

