
・どうして実効値は最大値を\(\sqrt{2}\)で割るの?
こんな悩みを解決します。
本記事の内容
- 実効値とは交流の平均値
- 最大値をルート2で割る理由とは?

交流回路になると、『瞬時値』や『実効値』など、新しい言葉が出てきて混乱してしまいますよね。
そこで今回は、どうして実効値は最大値を\(\sqrt{2}\)で割るのかについて話していきます。
前回の記事は【簡単】電気振動の解き方をわかりやすく解説【結論:単振動と同じです】を参考にどうぞ。
【電磁気の分野の注意点】
極力微積は使わないように説明していますが、電磁気の分野では微積を使うことで理解が深まる場所は、微積を使っています。
微積といっても、数Ⅱ数Ⅲの教科書例題レベルなので、身構えなくても大丈夫です!
【例】
・\(v=\frac{dx}{dt}\)
・・・(分子)の(分母)変化と読む。今回は、(位置)の(時間)変化なので、速度のこと
・\(a=\dot{v}=\ddot{x}\)
・・・ドットで微分を表す。2回微分であれば、ドットの数は2つ。
実効値は交流回路における平均値!

そもそも実効値は、交流回路における電流・電圧の平均値のことです。

どうして平均値が必要なのですか?
交流回路では、電流と電圧が時間変化するからなんだ!

交流回路の電圧は、
$$v=v_0sin\omega t$$
のように、時間変化するので、場所や時間によってばらつきが生じてしまいます。
それでは、計算ができないので、なんとか平均値を出せないか、という話になったのです。

なるほど。でも平均値ならなんで\(\sqrt{2}\)なんて中途半端な数で割るのですか?
それは、交流電圧の\(v=v_0sin\omega t\)のグラフを見ればわかるよ!

交流の平均はルートの2乗平均で求めよ!
$$(実効値)=\frac{(最大値)}{\sqrt{2}}$$
この公式になる理由を、グラフから見ていきましょう。
実効値は、交流回路における、電流電圧の平均の目安のことでしたので、平均値は『最大値と最小値の真ん中』になります。


えーっと、平均値は0ですか、、?
そんなわけないよね。
これは、グラフがマイナスの方向に飛び出してしまっているから、平均をとると0になってしまうんだ。


そうですよね。求めたいのは、交流電圧の大きさの平均値ですもんね。
大きさの平均値を求めたいから、下にはみ出ている部分を、何とか上にもって来れればいいよね!

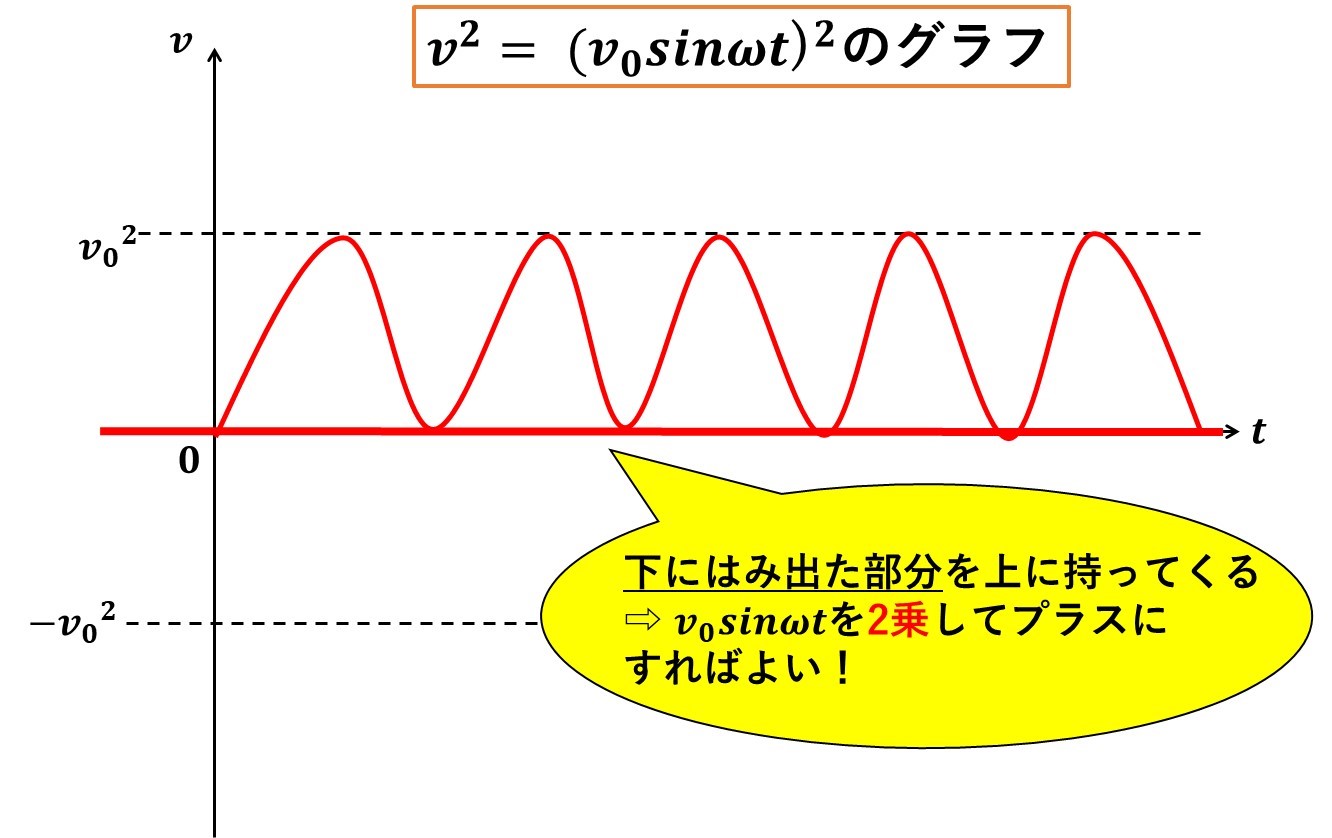

おお!すべて上にきました!けど、このままだと、\(v^2\)の平均値を求めてしまうことになりませんか?
そうならないために、実はここで、2乗を消すためにルートを使うんだよ!


すると、実効値が出てくるわけですが、やったことをまとめると下のようになります。
➀交流電流・電圧を2乗して大きさにする
➁2乗を消すために、ルートをつける
上の通りに計算してみると、
$$v=v_0sin\omega t$$
$$v^2=(v_0sin\omega t)^2$$
$$\sqrt{v^2}=\sqrt{{v_0}^2sin^2\omega t}$$
$$\sqrt{\overline{v^2}}=\sqrt{\overline{{v_0}^2}\overline{sin^2\omega t}}(平均をとる)$$
\(\overline{sin^2\omega t}\)は、\(sin^2\)関数の最大値が1で最小値が0だから、平均値は\(\frac{1}{2}\)になります。
$$\therefore V_e=\sqrt{{v_0}^2・\frac{1}{2}}$$$$=\frac{v_0}{\sqrt{2}}$$
となり、実効値は結果的に、最大値をルート2で割ったら出てくることがわかりました。
このような求め方を、2乗平均といいます。
思い返してみれば、熱力学の分子運動のところでも、2乗平均は使っていたよね!

まとめ:最大値をルート2で割る理由を覚えておこう!

今回は、実効値を求める時に、どうして最大値をルート2で割るのかについて話してきました。
ココがポイント
・2乗平均を用いて求めることができること
上の2つを知っていれば、『実効値って何だっけ?』ってなっても、最悪自分で求めることができます。
公式を暗記するのではなく、言葉の定義や理論を理解しておくことでより深く理解できますよ。
今回は以上です。
関連記事【差がつく!】交流回路に抵抗が繋がった問題の解き方を解説【簡単です】

