
電位の公式って2つあるから、ややこしくないですか?
確かにそうだね!けどそれは、公式を丸暗記しているからじゃないかな?

電位には、一様な電場における電位と、点電荷が作る電場における電位の式の2種類があります。
$$V=Ed$$
$$V=k\frac{Q}{r}$$
今回は、力学と比較しながら、一様な電場の公式の求め方について説明していきます!
電位とは+1[C]が持つ位置エネルギーだ!
最初に電位の定義について聞きたいんだけど、そもそも『電位』って何かわかるかい??


学校では、『高さ』のようなものと習いました!
回路問題を解くときには、その認識でもいいけれど、電位について議論するときに、それはまずいね!

受験生に、電位の問題がわかりませんという人がいますが、電位の定義について聞き返すと、答えられる人はほとんどいません。
そもそも電位とは、『+1[C]あたりが持つ静電気力による位置エネルギー』のことです!
単位は、"+1[C]あたりが持つ""位置エネルギー"なので、\([J/C]\)となりますが、これを\([V]\)(ボルト)といいます。
ポイント
・電位とは、『+1[C]あたりが持つ静電気力による位置エネルギー』のこと!
・単位は、\([J/C]=[V]\)(ボルト)
電位の定義について、しっかりと確認したうえで、次は2種類の電位について説明していきます。
電位の種類は2種類ある!
電位は、電場と同じように、『一様な場の電位』と、『点電荷が作る電位』の2つの種類があります!
これについても、力学と比較しながら見ていくよ!

一様な電場空間における電位
一様な場とは、地球のようにどこでも重力場が存在するような場のことを言います!
ここでは、
$$V=Ed$$
$$U=qEd=qV$$
の式を導出していきます!
まずは、力学で見ていきましょう。
電位の導出

上のように、重力場のある場所で、質量\(m\)のものを高さ\(h\)のところまで持ち上げると、その物体は
$$U=mgh$$
の位置エネルギーをもちますね!

言い換えれば、『基準に戻るまでに、重力が\(mg・h\)の仕事をする能力を持っている』ということになります。

重力が一定の力で働くから、仕事の公式の(力)×(距離)でエネルギーがわかるってことですね!
そうだね!重力場は一様な場だから、力の大きさはどこでも同じなんだ。

同じように電磁気でも考えていきましょう!
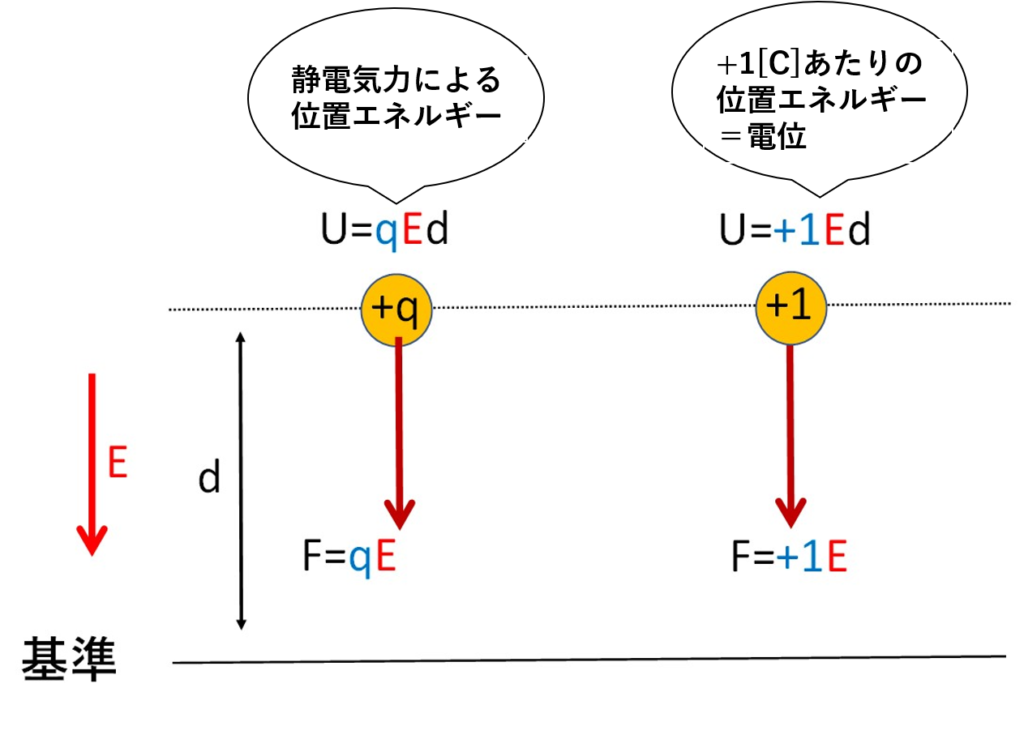
上のように、電場のある場所で、電荷\(+q\)のものを高さ\(d\)のところまで持ち上げると、\(+q\)は
$$U=qEd$$
の位置エネルギーを持ちます!

さっきの力学と似ていますよね!

また、最初にやったように、電位の定義は『+1[C]あたりが持つ静電気力による位置エネルギー』だったので、上の写真のように、電場の空間で、電荷\(+1[C]\)を、高さ\(d\)のところまで持ち上げると、その物体は
$$V=+1Ed$$
となります!
ポイント
・静電気力による位置エネルギーは、\(U=qEd\)
・電位は、上の\(qに+1\)を代入して\(V=Ed\)と書ける!
ところで、\(+q\)静電気力による位置エネルギーは、\(U=qEd\)と書けますが、そもそも\(+1[C]\)の持つエネルギーは\(V\)なのですから、\(+q\)の持つ位置エネルギーは、\(q×V\)となりますよね?
つまり、\(q×V\)と先ほど導いた、\(+q\)[C]が持つ静電気力による位置エネルギー
$$U=qEd$$
が等しいので、
$$q×V=qEd$$
$$V=Ed$$
となります!

なるほど!なんかすべてがつながった気がします!
電位の定義がわかれば、\(+q[C]\)の持つ位置エネルギーを求めるのは簡単だね!

まとめ

今回は、力学と比較しながら、一様な電場の公式の求め方について理解してきました!
今回の記事で、『どのようにして電位ができているのか』理解することができましたか?
電位の導出は、電磁気の理解に非常に重要なので、何度もノートに書いて、何も見なくても友達に説明できるようになりましょう!
電位にはもう一つ、『点電荷が作る電位』があります。
点電荷の電位の式にマイナスが付く理由や、電位の基準を無限遠点にとる理由については以下の記事を参考にしてみてください。
今回は以上です。
関連記事点電荷の電位を無限遠に基準をとる理由【マイナスになる原因も解説します】


