
・運動量と力積の関係の式の使い方がわからない
・そもそも使う場面がわからない
今回は、上のような疑問を解決していきます!
この記事を読めば、運動量と力積の関係の式の使い方がわかるので、力学全体の問題への理解が深まりますよ!
✔この記事の内容
・運動量と力積の関係の式の使い方
・運動量の問題の解き方
・式を立てるための条件
この記事の信頼性
浪人時に、勉強法と思考法を変えただけで、記述模試偏差値65以上、センター試験満点近くまで伸ばした『考え方』や『解き方』をギュっと凝縮してまとめています。
運動量と力積の関係のまとめ

前回、運動量と力積の関係は、以下のようであるとわかりましたね。
ココがポイント
・仕事は、力がどのくらいの距離移動したかで、力積は、力をどれくらいの時間かけたか
・運動量と力積の関係の式は、主に2地点の時間が与えられた(欲しい)ときに使う
以上の内容を踏まえて、さっそく例題を見ていきましょう。
例題
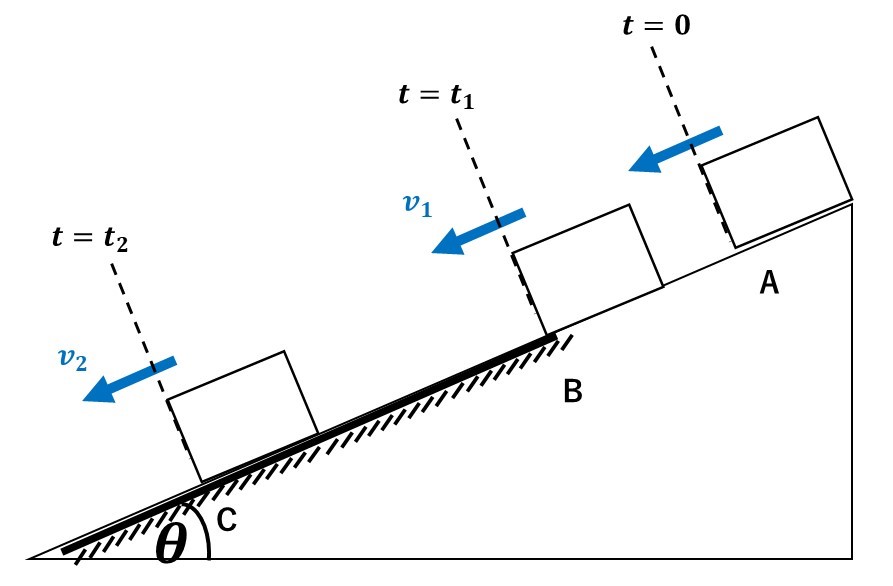
図に示すような、水平面となす角\(theta\)の斜面を、質量mの小物体が滑り降りるような運動を考える。小物体をAの位置から静かに放すと、小物体は、斜面を滑り、点Bを通って静止しないで点Cを通過する。Bよりも情報はなめらかな斜面で、Bより下方は動摩擦係数\(\mu'\)の粗い面とする。重力加速度を\(g\)として、点Bを通過する時刻\(t_1\)tと点Cを通過するときの速さ\(v_2\)を求めよ。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
問題の解答
さて、最初はどうしようか。


力学の問題は、まずは運動方程式ですよね!
なめらかな斜面と、粗い斜面の2つにおいて、運動方程式を立てると、以下のようになります。
$$【なめらかな斜面】ma=mgsin \theta$$$$【粗い斜面】ma=mgsin \theta -\mu' mgcos \theta$$

加速度\(a\)がいずれも一定なので、等加速度の式3本か、エネルギー保存の式、どれかが使えそうです!
いいね~!けれど、残念。それではかなり面倒な式になるよ。


どういうことですか?
今回、問題文には距離の情報が書いていないから、高さ変化や距離の変化を使う式が使えないんだ!


それじゃ、どうすればいいのですか?
今回は、距離の代わりに、時刻が書いてあるので、運動量と力積の関係の式が使えるよ!

ココがポイント
運動量と力積の関係の式が、運動方程式から導けたことを利用して、式を立てていくよ!

運動方程式を見ながら、運動量と力積の関係の式を立てていきましょう。
左辺は、2点の運動量変化、右辺には力がかかった時間を書いていけばOKだよ!




わ!運動方程式から一発で式が立ちました!
2地点の時間と速さがわかれば、簡単に式を立てられるね!

$$mv_1=mgsin\theta t_1-0 t_1$$
$$mv_2-0=mgsin\theta t_2-\mu 'mgcos\theta (t_2-t_1)$$
この式を解いて、\(t_1\)と\(V_2\)を求めて、
$$T_1=\frac{v_1}{gsin \theta}$$$$v_2=gt_2sin\theta-{\mu}'t_2gcos\theta+\frac{{\mu}'g}{tan\theta}$$
となります!
まとめ:運動量と力積の関係を使う場面を覚えよう!

今回は、運動量と力積の関係の式の使い方について話してきました。
使い方と、式の立て方については、以下のとおりです!
運動量と力積の関係
・運動量と力積の関係の式は、2点間の時間を求めたい(知りたい)ときに使う。
・運動方程式を立てて、左辺に運動量変化、右辺の力に時間をかけた時間をかける。
以上のことに気を付けながら、力学の問題を考えると、運動量と力積の関係の式の立てるべき場面がわかりますので、自分の持っている問題集で、確認してみてください!

