
・電気振動って何?
・周期の求め方がわからない
・LC回路の解き方がわからない
こんな悩みを解決します。
✔この記事の内容
・電気振動はシャトルラン
・電気振動の周期は単振動
・暗記しないLC回路の解き方
✔この記事の信頼性
苦手だった物理を、浪人時に偏差値65以上センター試験満点近くまで伸ばした、参考書には書かれていない、考え方や勉強法について、必要なエッセンスを『ぎゅっと』凝縮してまとめています。
今回は、電気振動の解き方と攻略法について解説していきます。
コイルが出てくると、電磁気が苦手になる人とても増えてきます。
しかも、電気振動の話は、物理のエッセンスにも詳しく書かれていないので、『どうしてこの式が出てくるの?』みたいな疑問がわくことも多いのではないでしょうか。
本記事で紹介する方法を使えば、電気振動の問題は誰でも簡単に解けるようになります。
記事の後半では、例題を踏まえつつ電気振動の解き方についてわかりやすく解説していくので最後までじっくり読んでみてください!

それではさっそくみていきましょう。
前回の記事は【難関大必須】ファラデーの法則を完全理解【問題の解き方を徹底解説】を参考にどうぞ。
【電磁気の分野の注意点】
極力微積は使わないように説明していますが、電磁気の分野では微積を使うことで理解が深まる場所は、微積を使っています。
微積といっても、数Ⅱ数Ⅲの教科書例題レベルなので、身構えなくても大丈夫です!
【例】
・\(v=\frac{dx}{dt}\)
・・・(分子)の(分母)変化と読む。今回は、(位置)の(時間)変化なので、速度のこと
・\(a=\dot{v}=\ddot{x}\)
・・・ドットで微分を表す。2回微分であれば、ドットの数は2つ。
電気振動は電荷がシャトルランする現象

電気振動とは、電荷をもったコンデンサーにコイルをつなぐことで起こり、コンデンサーに蓄えられた電荷が、回路内をシャトルランする現象です。
つまり、電荷が『逆側の極板に移動して、また戻ってくる』というのをひたすら繰り返す、鬼のような運動なのです。

いわば、無限シャトルランですね
では、どのようにして電気振動は起こるのでしょう。
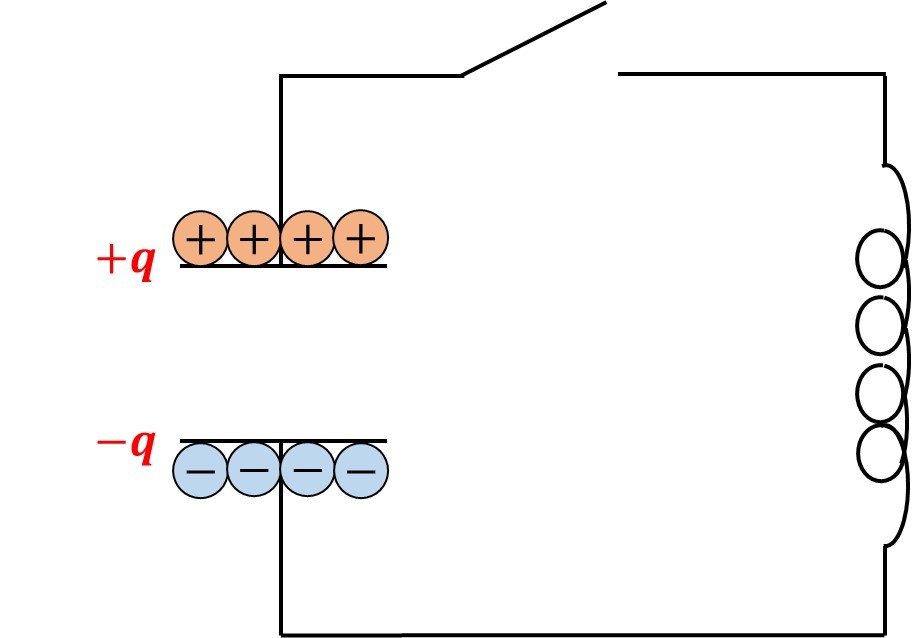
最初は、上みたいにコンデンサーが持っていて、スイッチが開いている状態です。
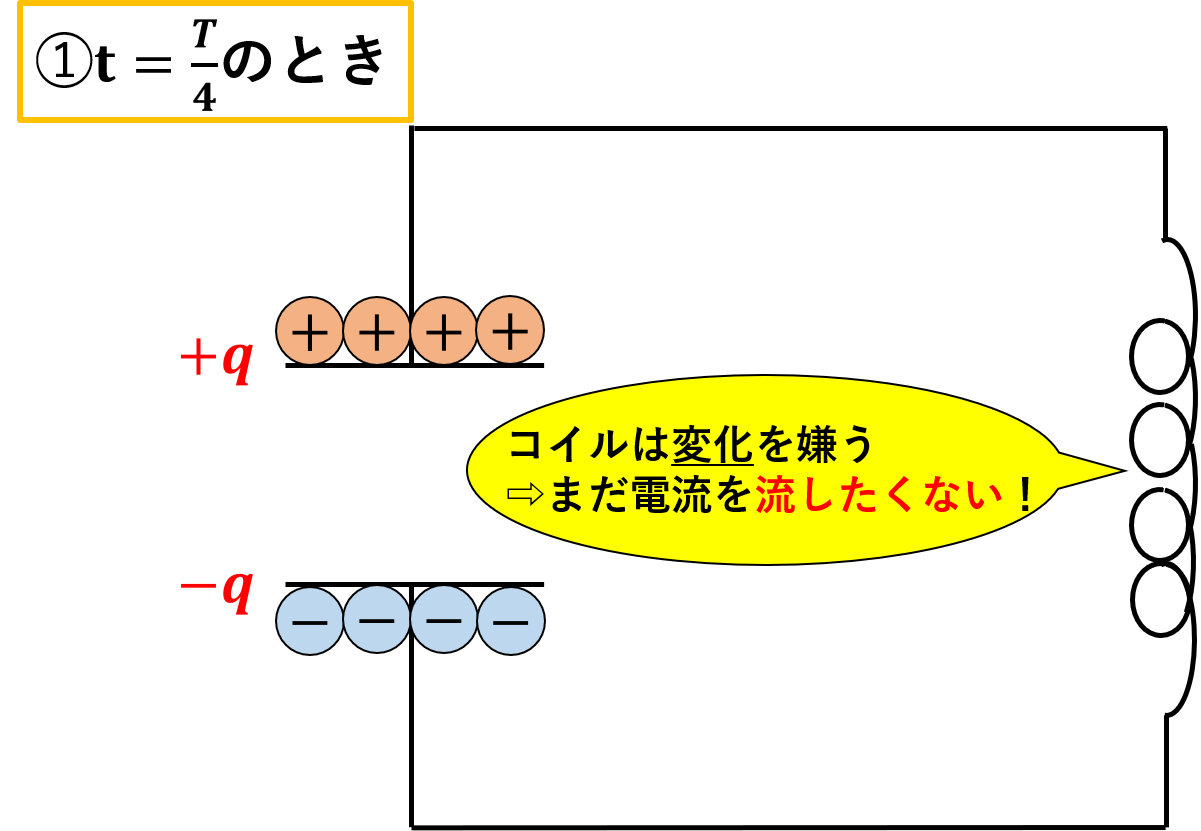
スイッチを閉じると、コンデンサーに溜まった電荷が放出されますが、コイルは環境の変化を嫌うので、もともと電流が流れていなかった回路に電流を流そうとはしません。
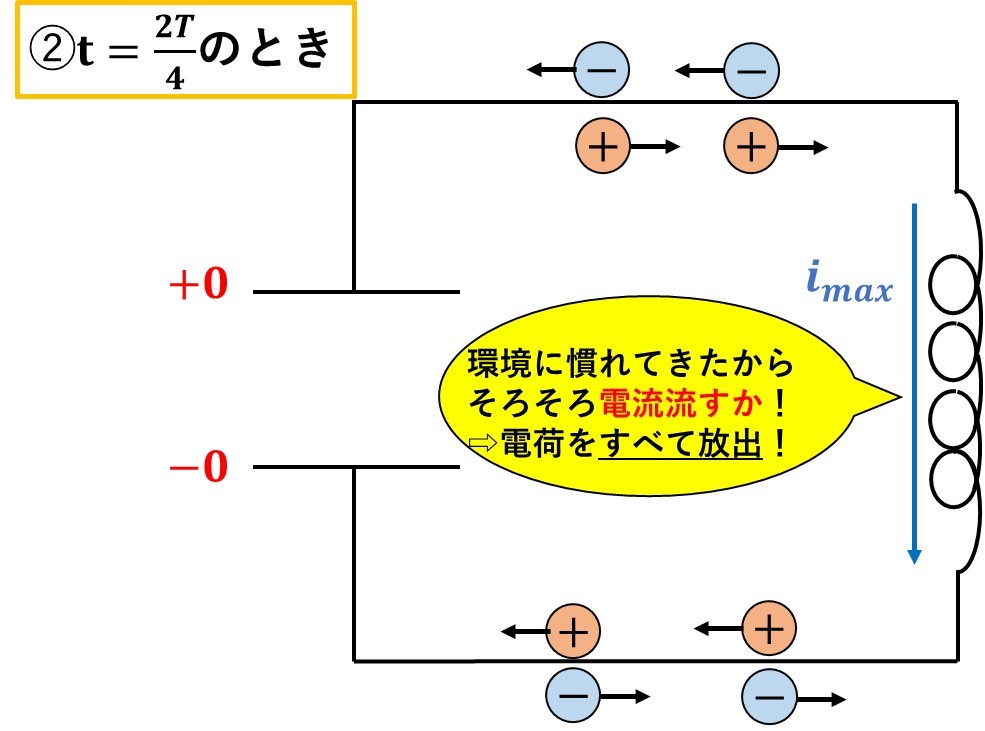
さらに、\(\frac{T}{4}\)秒経つと、コイルも環境に慣れてくるので、電流を流すようになります。
この時、コンデンサーに溜まっている電荷すべてを放出するので、電流は最大になります。
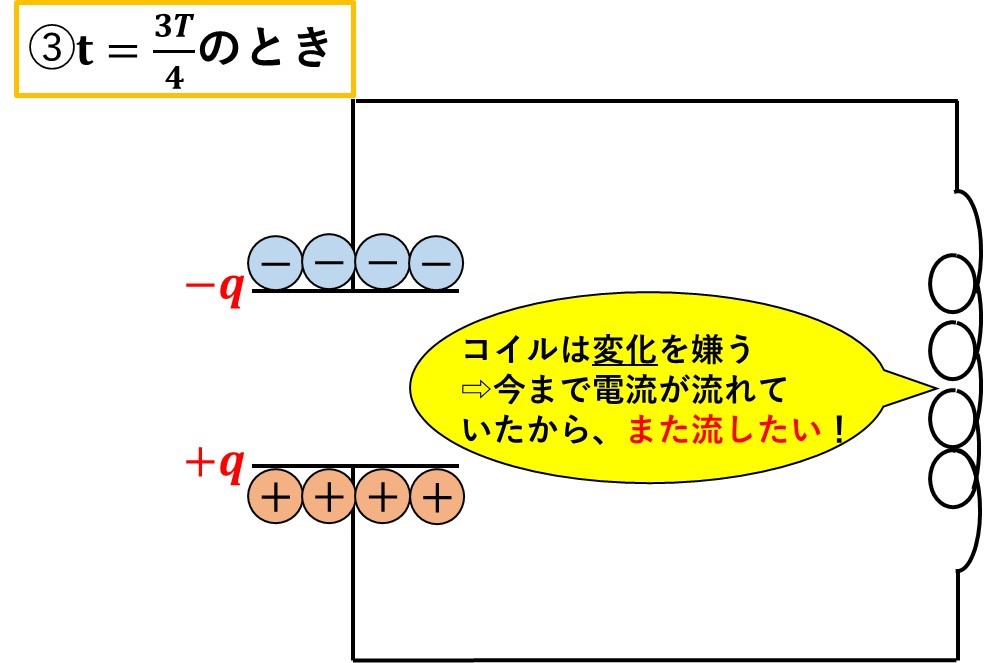
さらに、\(\frac{T}{4}\)秒経つと、電流が流れ切って、電荷が反対側の極板に溜まりますが、コイルは環境の変化を嫌うので、さっきまで流れていた電流を、また流そうとします。
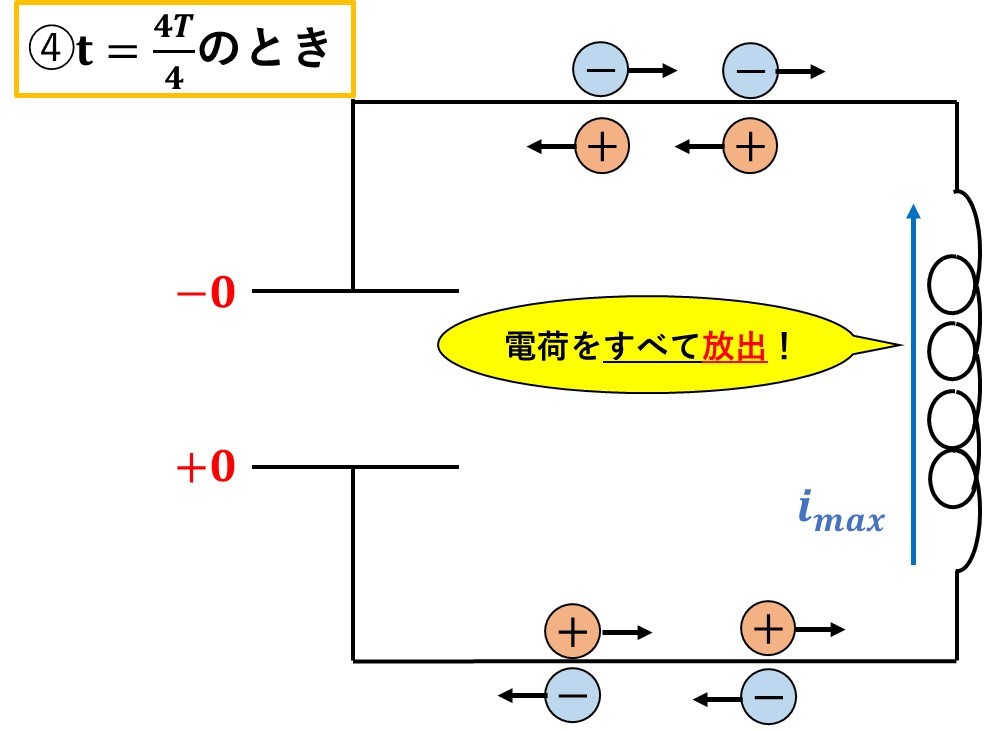
さらに、\(\frac{T}{4}\)秒経つと、コイルはコンデンサーに溜まった電荷を、すべて流し始めるので、再び電流は最大になります。

そして、また最初の状態に戻って、\(\frac{T}{4}\)秒おきに上の変化が繰り返されます。
これが、電気振動という現象です。

コイルってなんだか面倒ですね
電気振動の周期は単振動と同じように求められる
電気振動は、上のように周期を4つに分けて現象を説明できますが、1周期は
$$T=2\pi \sqrt{LC}$$
のように表せます。
実は、覚える必要はなく、単振動の問題が解ければ、式の形が同じになるので、簡単に導くことができます!
単振動の加速度は、下のように表せましたね!

単振動の加速度
$$a=-{\omega}^2(x-x_0)$$$$\ddot{x}=-{\omega}^2(x-x_0)$$
ここで大切なのは、『\(\ddot{x}\)が\(x\)のマイナス一次間数のときは、単振動型』になるということです。
このことを踏まえたうえで、例題を見ていきましょう。
電気振動の例題&解き方
例題

コンデンサーの容量が\(C\)、コイルの自己インダクタンスを\(L\)とした時、電気振動の角周波数\(\omega\)、周期\(T\)、振動中心を求めよ。ただし、最初コンデンサーには、\(+q\)の電荷が溜まっているものとする。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは、解説していくよ!

例題の解説
電磁気の回路問題は、解き方が決まっていましたね!
回路問題の解き方
➁オームの法則を使って抵抗にある未知数を求める
➂回路方程式を立てて、電荷や電流を求める
※回路方程式とは、キルヒホッフの法則(電流保存、電位1周で電位差0)や電荷保存の式のこと
さらに、回路の中にコイルがあるときは、『仮定した電流とは逆方向に、誘電起電力\(L\frac{dI}{dt}\)』を取ってあげればよいのでした。
※知らなかった人は【RC回路はこう解け!コイルの入った回路問題をわかりやすく解説!】をチェック!
・➀で、電流を仮定する(このとき、コイルの誘電起電力を定める)
・➁は抵抗がないからやらない(代わりにコンデンサーにかかる電圧を描く)
上のように考えると下のようになります。
➂の、『電圧1周の電位差は0』を使って回路方程式を立てると、
$$L\frac{dI}{dt}=\frac{q}{C}・・・➀$$
となります。
式は1本では解けませんので、もう1本式が欲しいところですが、電荷保存、電流保存は使うことができません。
こんな時は、電荷保存の式(時間変化ver)を使うよ!


詳しくは、【参考書に書かれていない電荷保存則の時間変化版について解説】をご覧ください。

今回は、コンデンサーの\(+q\)から電流が出ていっているので、放電となり、符号はマイナスになります。
電荷保存の時間変化の式を書くと、
$$i=-\frac{dq}{dt}=-\dot{q}・・・➁$$
となります。
$$L\frac{dI}{dt}=\frac{q}{C}・・・➀$$$$i=-\dot{q}・・・➁$$
➁の\(i\)を➀の\(di\)に代入して
$$L\frac{d(-\dot{q})}{dt}=\frac{q}{C}$$
$$L\frac{d}{dt}(-\dot{q})=\frac{q}{C}$$
$$-L\ddot{q}=\frac{q}{C}
(微分したので、ドットが増える)$$
$$\therefore \ddot{q}=-\frac{1}{LC}q$$
と変形できます。

あ!単振動の式と形が似ています!
『\(\ddot{q}\) が\(q\) のマイナス一次間数のときは、単振動型』になるのでしたね!

$$\ddot{x}=-{\omega}^2(x-x_0)$$$$\therefore \ddot{q}=-\frac{1}{LC}(q-0)$$
角振動数が\(\omega\)、振動中心が\(x_0\)なので、比較すると
角周波数$$\omega=\sqrt{\frac{1}{LC}}$$
周期
$$T=\frac{2\pi}{\omega}=2\pi\sqrt{LC}$$
振動中心$$q=0$$
の電気振動であることがわかります。
こんな感じで、回路問題を解くやり方で、勝手に答えが出てくるんだ!

まとめ:単振動と比較すれば電気振動は簡単に解ける!

今回は、電気振動の周期の求め方について話してきました。
電気振動は、『\(\ddot{q}\) が\(q\) のマイナス一次間数の単振動型』になるので、単振動の加速度と比較することで、簡単に周期を求めることができます。
この解き方を覚えてしまえば、どんな問題でも解くことができますのでしっかりできるようにしておきましょう。
今回は以上です。
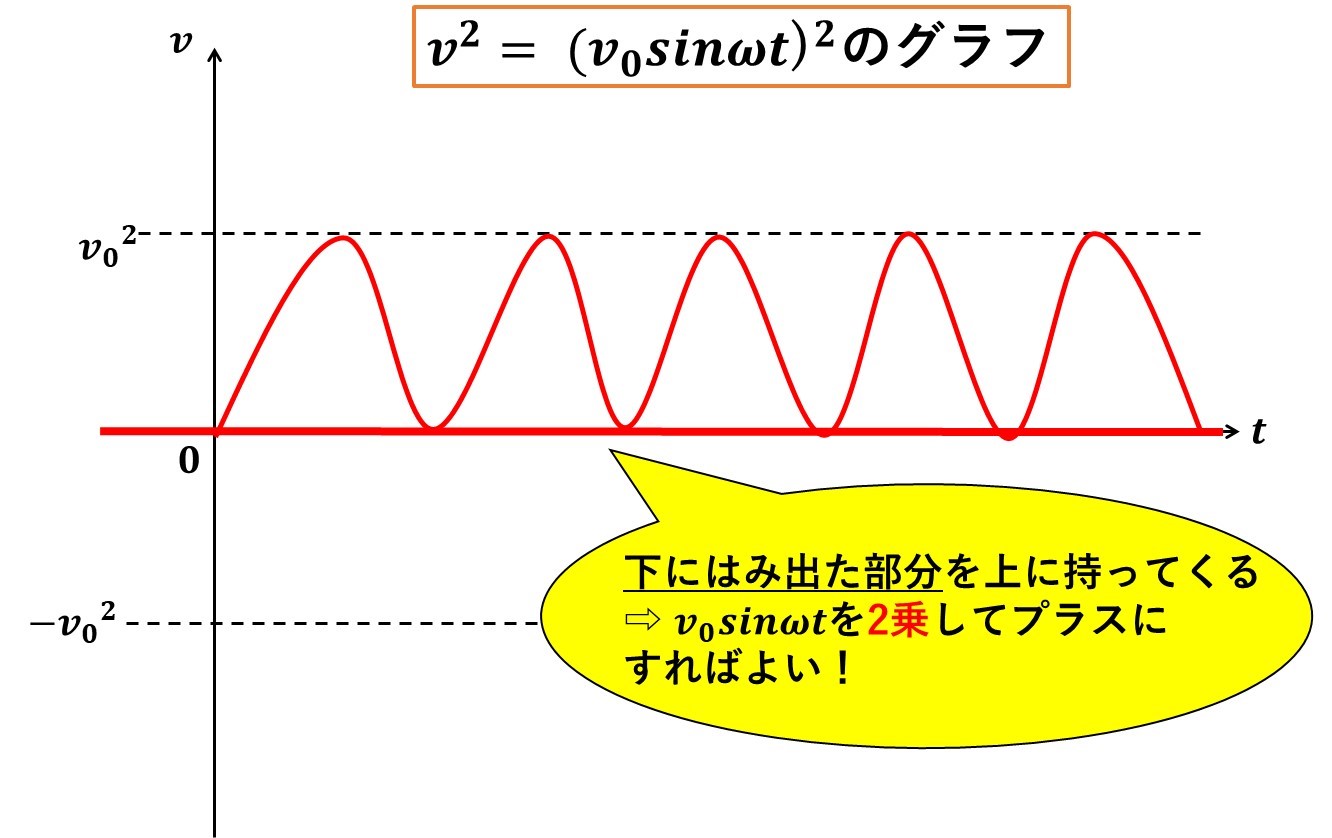
関連記事実効値はどうしてルート2で割るの?【結論:平均値を求めているだけです】


