
電磁気の回路の問題って、どうやって解いたらいいかわからないし、式の立て方もわかりにくいんだよねー
確かに、電磁気の回路の問題は、やることがたくさんあるように見えるので、複雑になりがちですよね。
ですが、コンデンサーや抵抗の回路の問題では、回路方程式と呼ばれるたった3本の式を立てるだけで、簡単に解くことができます。
そこで今回は、そんな電磁気で立てるべき回路方程式について紹介していきます!
前回の記事は【攻略】電磁気の回路問題の解き方はたった1つ【結論:回路問題はヌルゲーです】を参考にどうぞ。
まず最初に知っておくこと!
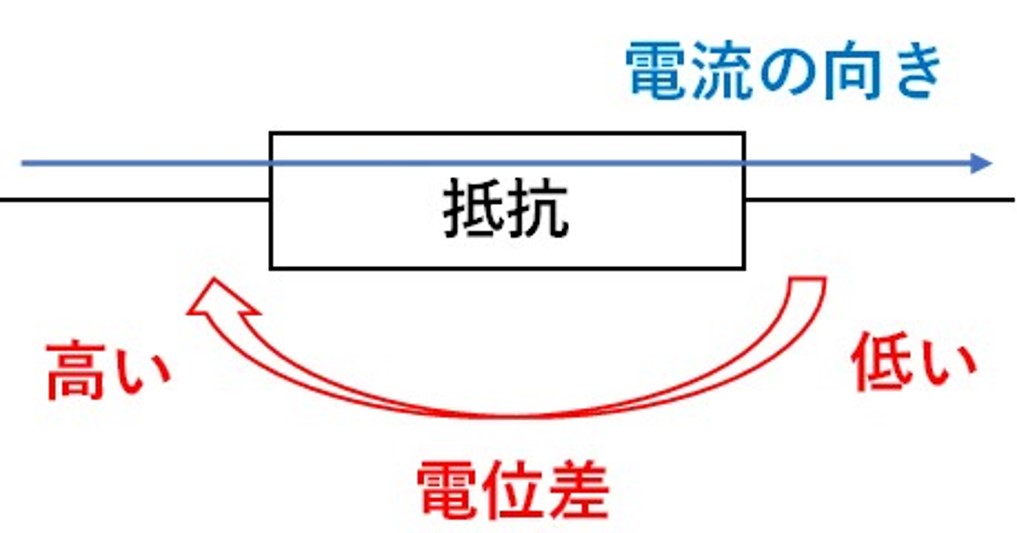
回路問題の解き方について紹介する前に、まずは問題を解くための、作図の仕方について紹介します!
この作図を必ずやることが、回路問題を正確に解くコツにもなりますので、しっかりと覚えておきましょう。
作図のポイント
・電流の流れを矢印を使って書く!
・電圧は高い方(高電位の方)を矢印の先端にして書く!
1.電流
電流とは、簡単に説明すると、『電子の流れ』のことです。
電流は、よく『水の流れ』に例えられ、水と同じように電流も、高いところから低い方へと流れていきます。
つまり、電位差(回路の高低)がわかれば、自動的に電流の流れる方向がわかってしまうのです!
このサイトでは、電流の流れを『青矢印』で書いていますので、自分でもしっかり描けるようにしましょうね!
電位(電位差)
回路内は、電池などの装置によって、電気的な高低差が生じています。
この電気的な高さのことを、『電位』と呼び、高さの差のことを『電位差』といいます!

電位の差のことを電位差というので間違えないように注意!
このサイトでは、電位差を高い方の電位を先端にして、『赤矢印』で作図していくので、皆さんも作図していってください!
つまり、矢印を作図することで、矢印の先端が高電位だということがわかるのです!
回路方程式とは??
続いては、回路方程式について紹介していきます!
回路方程式
1.電荷保存の式
2.電流保存の式(キルヒホッフの第一法則)
3.任意のループ1周での電位の関係式(キルヒホッフの第二法則)
一つずつ説明していくから、読み飛ばさないでね!

1.電荷保存の式
電荷保存の式とは、回路内にコンデンサーがあるときに使えます。
この式は、『スイッチをつなげた』などの、ある操作をした時に、その操作前後で電荷がどのように変化したのか、という電荷の変化を見ます。
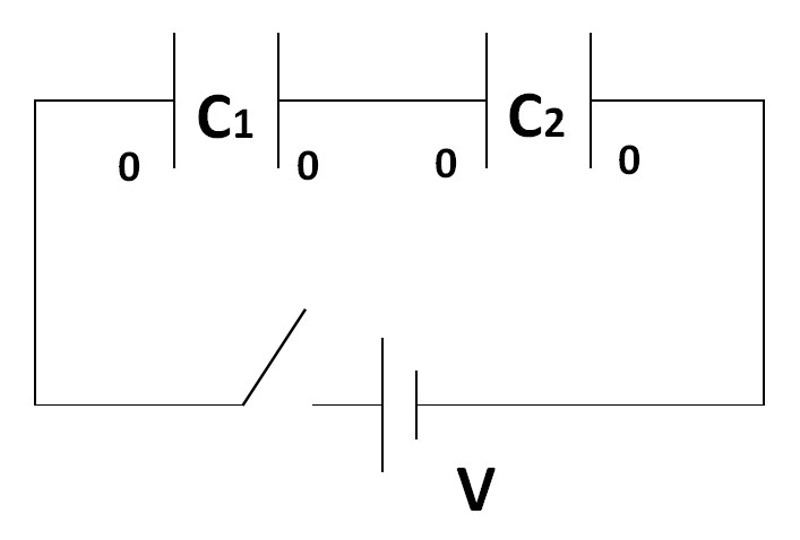
例えば、このような回路があったとします。
写真を見ると、スイッチがつながっておらず、コンデンサーには電荷はありません。
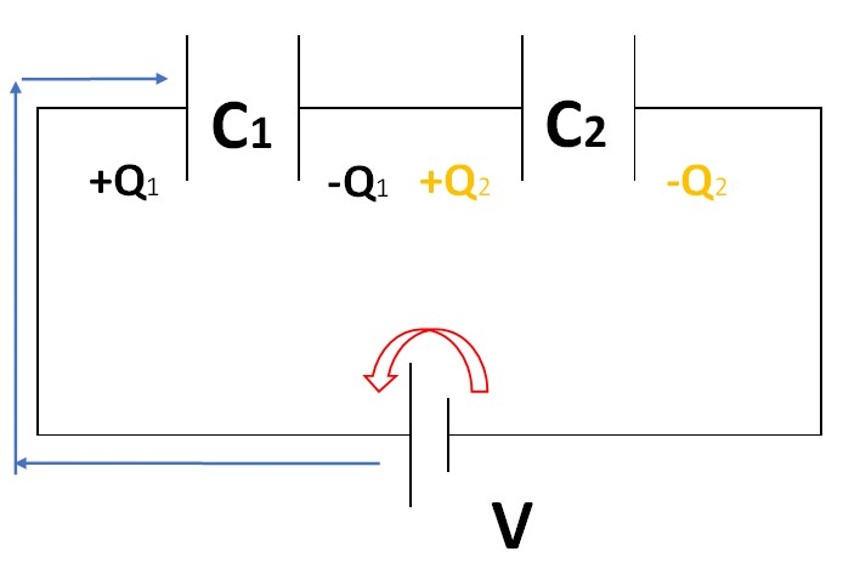
スイッチを繋ぐと、コンデンサーに電流が流れ込み、流れ込んできた方のコンデンサーの方には、プラスの電荷が溜まります!
この電荷の大きさを、+Q1と自分で置きます。
その時、反対側のコンデンサーには、符号が逆向きで大きさが同じ電荷が溜まりますね!
この時、もう一つのコンデンサーにも電荷が溜まりますので、自分で\(+Q_2\)と置き、反対側には\(-Q_2\)とおきます。
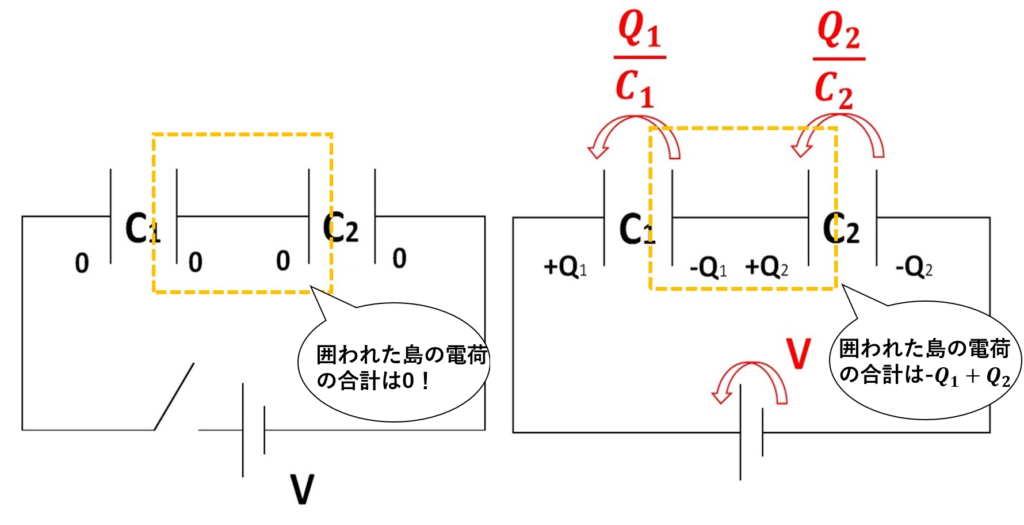
このように、コンデンサーに電荷が溜まっているときに、電荷保存の式を使います!
電荷が保存するのは、コンデンサーの孤立系です。
孤立系は、コンデンサーの島のような部分で、導線とつながっていないため、孤立系では電荷が保存するのです!

コンデンサーの島(オレンジで囲ったところ)の中では、電荷が動作前後で保存します。
よって、電荷保存の式は、左辺をスイッチをつなぐ前の電荷、右辺をスイッチをつないだ後の電荷として、
$$0+0=-Q_1+Q_2・・・➀$$
と書くことができます!
電荷保存の式を立てるためには、上のように『動作前後の図』が必要になりますので、図は必ず操作するごとに描くようにしましょう!
2.電流保存の式
電流保存の式は、キルヒホッフの第一法則とも呼ばれ、『流入する電流の総和と流出する電流の総和は0(ゼロ)』という法則です!

なんか難しそう、、、
と思ってしまいがちですが、そんなことはありません!
電流は水の流れと一緒なので、『回路の中に枝分かれがあれば、電流はどちらにも流れる』といっているだけ!
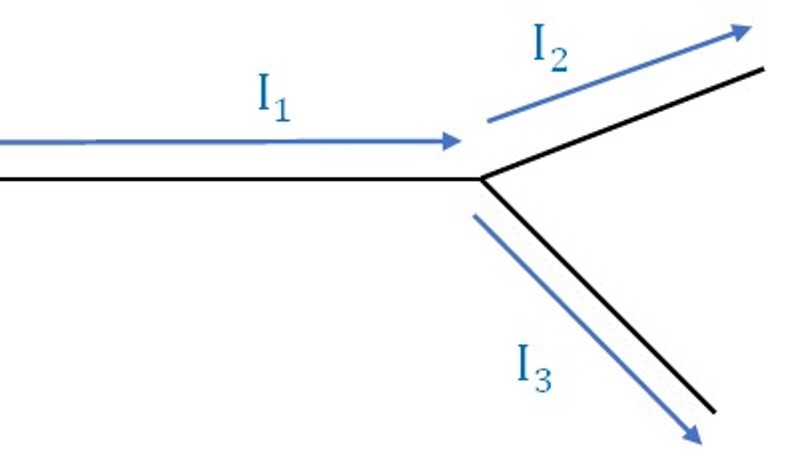
上の図は、回路のある一部分を切り取ったものです。
回路の途中で枝分かれが発生して、電流は2つの道に流れていますね。
電流は、勝手に湧き出したりしないので、電流は
$$I_1=I_2+I_3$$
という保存の関係になります!
これが2つ目の式である、電流保存の式です!
3.任意のループ1周での電位の関係式(キルヒホッフの第二法則)
最後は、キルヒホッフの第二法則です!

キルヒホッフの第一法則とどう違うの??
キルヒホッフの第一法則は、電流に関する法則だったけれど、第二法則は電位に関する法則なんだ!

回路は、任意のループで一周して同じ場所に戻ると、電位の変化は0になります!
例えば、ショッピングモールに行ったとしましょう。
一階のある場所から、エスカレーターを使って2階3階と上がって、同じ場所に戻ってこようとしたら、必ず上った分だけエスカレーターで下がりますよね。
つまり、何階まで上ろうとも、同じ場所に戻ってきたら、高さの変化は0になります!
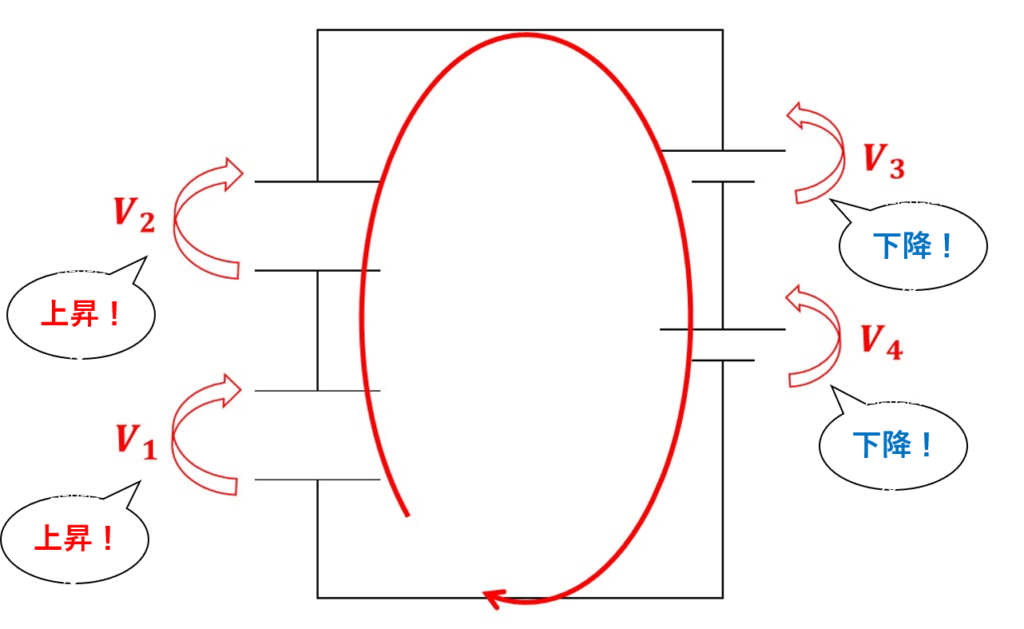
上の図を見てみると、ループでがありますので、赤矢印のようになぞっていきましょう!
回路を一周なぞったときに、矢印の根元から先端に向かってなぞれば上昇。
逆に、先端から根元に向かってなぞれば、高さは下降です!
最初の\(V_1\)は、根元から先端なので、上昇です。

同じように考えていくと、写真のように上昇と下降を繰り返して、元の場所に戻ってきます。
上昇をプラス、下降をマイナスとして、式を立てると、
$$+V_1+V_2-V_3-V_4=0$$
となります。
よく受験生で、どっちが高電位かわからない図を描いている人がいますが、それは符号を間違える可能性があるので、絶対にやめましょう!
物理は、符号のミスが命取りになる科目ですので、図は『きれいに、なおかつ、わかりやすく』書きましょうね!
まとめ
今回は、電磁気の回路問題を解くときに立てる、3つの回路方程式について紹介しました!
今回の内容をまとめると、下のようになります。
回路方程式
1.電荷保存の式
⇨孤立系(コンデンサーの島)の中で、電荷の変化を見る!
2.電流保存の式(キルヒホッフの第一法則)
⇨回路の中で枝分かれがあれば、電流保存!
3.任意のループ1周での電位の関係式(キルヒホッフの第二法則)
⇨任意のループを考えて、一周したときの電位変化は0!
この3つの式を覚えて、しっかりと作図を行えば、回路問題は簡単に解くことができます!
自分の手を動かして、自分の問題集で試してみてくださいね。
今回は以上です。
関連記事磁場と磁束密度は違いとは?【約9割の受験生が知らない落とし穴】


