
電磁誘導ってどうして起こるのですか?
実は、回転する電場が発生して、それが電荷を移動させているからなんだ!

今回は、受験生がつまずきやすい、電磁誘導について説明していきます!
そして最後には、以下の例題が解けるようになりますので、しっかり勉強していきましょう。
例題
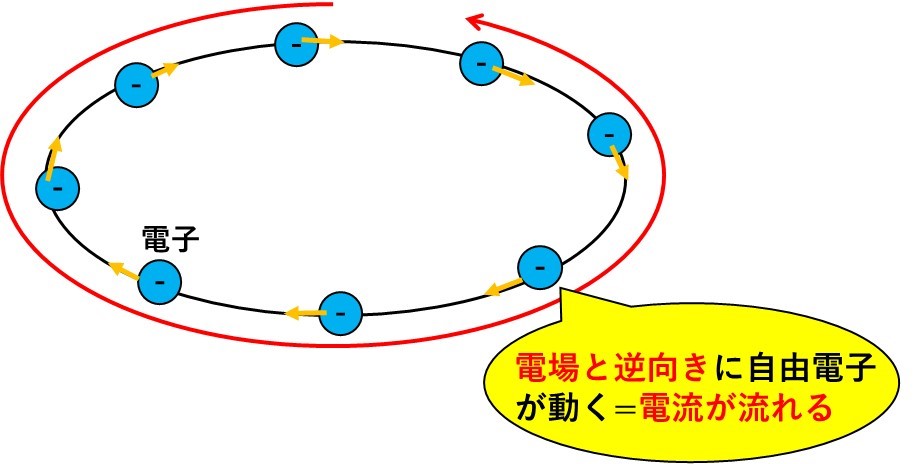
【問】図の向きを正とした時、電磁誘導で生じた電流は、どれくらいか答えなさい。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
前回の記事は磁場と磁束密度は違いとは?【約9割の受験生が知らない落とし穴】を参考にどうぞ。
目次
電磁誘導とは発生する電場によって電荷が運ばれる現象

電磁誘導とは、周りの磁界が変化することで、回路の中に電流が流れる現象のことです!
じゃあどうして、電磁誘導が起こるかわかるかい?


えーっと・・・
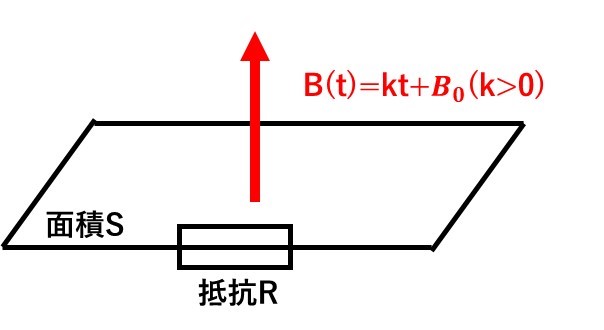
実は、電磁誘導が起こるのは、空間の磁場(磁束)が時間変化すると、その周りを取り囲むように回転する電場(誘導電場)が生じるからなんだ!
ポイント
電磁誘導は、空間の磁場(磁束)が時間変化すると、その周りを取り囲むように回転する電場(誘導電場)が生じることが原因
これめっちゃ大事なので、覚えておいてください!!

でもどうして、回転する電場が発生すると、電流が流れるのですか?
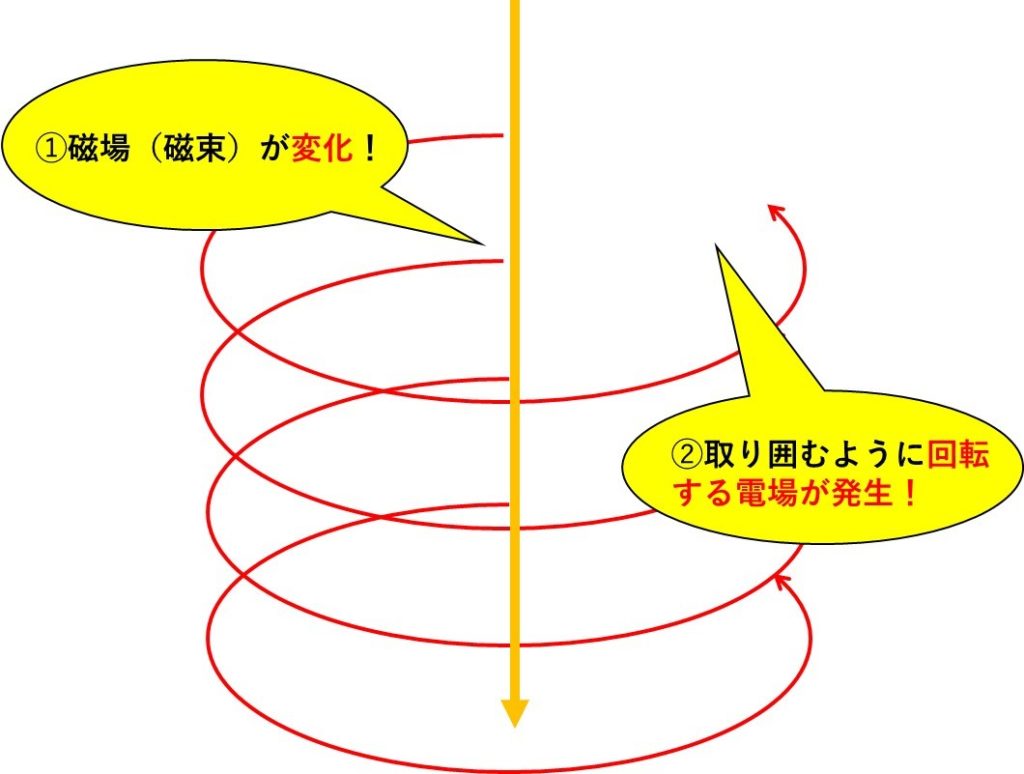
コイル内部には、金属だから自由電子がたくさんあるよね。その電子たちが、回転する電場からクーロン力をうけて、運ばれるからなんだ!

コイル内の自由電子が流れて、電流が流れるということは、コイルには当然起電力が生じているとみることができます。
この起電力のことを、誘電起電力といいます!
誘電起電力が起こる理由
➀空間の磁場(磁束)が変化する!
➁その周りを取り囲むように回転電場(誘導電場)が発生!
➂誘導電場によってコイル内の自由電子が運ばれ、電流が流れる!
➃電流が流れているので、起電力(誘電起電力)が生じていることがわかる!
※上で説明した内容は、参考書にも書いていないので、しっかりと覚えておきましょう!!!

つまり、磁束が変化したことによって、誘導起電力が生じたのですね!
それを式にすると、下のようになるよ!

誘電起電力をVとすると、Vは磁束\(\Phi\)の時間変化によって生じたのだから、
$$V=\lim_{\Delta t\rightarrow0}\frac{\Delta\Phi}{\Delta t}=\frac{d\Phi}{dt}$$に比例し、
$$V=|\frac{d\Phi}{dt}|$$と書けるのです!
これを、ファラデーの電磁誘導の法則といいます。
ファラデーの電磁誘導の法則
誘電起電力をVとすると、Vは磁束\(\Phi\)の時間変化によって生じるので、
$$V=|\frac{d\Phi}{dt}|$$と書ける

誘電起電力が生じる理由は、分かりましたけど、どうして起電力に絶対値がついてるのですか?
それは、起電力の向きが、磁束の変化によって変わるからなんだ!その法則をレンツの法則というよ!

電磁誘導の向きを決めるレンツの法則
電磁誘導の向きは、レンツの法則によって決まります!
レンツの法則
・起電力の向きは、磁束\(\Phi\)の変化を妨げようとする向き(右ネジの向き)
例えば、下のような状況を考えてみよう!


例えば、上向きに磁束が増えると、それを減らそうと下向きの磁束が生まれます!
その時に、右ネジを回す方向に、誘電起電力が発生するのです。このようにして、誘電起電力の向きは決めることができます!
ポイント
➀磁場が変化する
➁変化(増加、減少)の向きを妨げる方向に対して、磁束が発生する。
➂妨げる方向に、右ネジの先端を向けて、回した方向に電流(誘電起電力)が生じる。
例題の解説:電磁誘導とレンツの法則
例題

【問】図の向きを正とした時、電磁誘導で生じた電流は、どれくらいか答えなさい。
それでは解説していくよ!まずは電磁誘導の大きさから求めていこう。

電磁誘導の大きさ
ファラデーの電磁誘導の法則
誘電起電力をVとすると、Vは磁束\(\Phi\)の時間変化によって生じるので、
$$V=|\frac{d\Phi}{dt}|$$と書ける
電磁誘導の大きさは、上のような式で求められるのでした。

磁束\(\Phi\)は$$\Phi=BS$$で求められるので、
$$\Phi=BS$$$$=(kt+B_0)S$$$$=kSt+B_0S$$となります。
これを、\(V=|\frac{d\Phi}{dt}|\)に代入して、
$$V=|\frac{d\Phi}{dt}|$$$$V=|\frac{d}{dt}(kSt+B_0S)|(tで微分する)$$$$=|kS+0|$$$$=kS$$となります。
電磁誘導の向き

電磁誘導の向きは、レンツの法則より磁束の変化を妨げる向きでした。
上の図を見ると、k>0となっていることから、上向きに増えていることがわかります!
よって、下向きに磁束を発生させる必要があるので、ネジの先端を下に向けると、右ネジの法則より誘電起電力は、時計回り発生します。
よって、答えは時計回りになります。
まとめ:電磁誘導を理解すれば受験で圧倒的に有利!
今回は、電磁誘導が発生する原理と、レンツの法則について説明しました!
このあたりから、微分が出てきたりするので、苦手な人が増えてきますが、そんなに難しい計算問題は出てこないので、少しずつ慣れていきましょう。
ところで、こんな電磁誘導の問題はどうでしょう。
例題

紙面上に金属線が、図のようにねじれた形で置いてある。金属線の表面は絶縁体の被膜でおおわれており、全体の抵抗値はRである。鉛直上向きに一様な磁束密度\(B(t)=ksin(wt)+B_0\)の形で時間変化する磁場を加えた。この時、コイルに流れる電流を求めよ。ただし、電流の向きは、図の方向を正方向とする。
この問題は、東京工業大学の問題ですが、難しいのは『磁束密度が時間によって変化する』ということです。
増える、減るがわかれば、レンツの法則から誘電起電力の向きがわかりますが、この場合ではわかりません。
そこで『そんな時はどうするのか』ということについて、次回は説明していきます!

