いきなりだけど、今回は次のような問題を考えていくよ!

例題

紙面上に金属線が、図のようにねじれた形で置いてある。金属線の表面は絶縁体の被膜でおおわれており、全体の抵抗値はRである。鉛直上向きに一様な磁束密度\(B(t)=ksin(wt)+B_0\)の形で時間変化する磁場を加えた。この時、コイルに流れる電流を求めよ。ただし、電流の向きは、図の方向を正方向とする。
この問題は、東京工業大学の問題ですが、難しいのは『磁束密度が時間によって変化する』ということです。
増える、減るがわかれば、レンツの法則から誘電起電力の向きがわかりますが、この場合ではわかりません。
そこで『磁束変化の向きがわからない時はどうするのか』ということについて、今回は説明していきます!
※今回の内容は、主にMARCHよりも上を受験する人向けになっています。知っていると得ですが、MARCH以下なら前回の解き方で解けることが多いので、見なくても大丈夫です。
⇨前回の内容は電磁誘導とレンツの法則って何?【参考書に載ってない原理から解説】を参考にどうぞ。
目次
ファラデーの法則(レンツの法則を内包した形)を使う!
前回、磁束が変化すると、ファラデーの電磁誘導の法則に従って、誘電起電力の大きさが決まるのでした。
ファラデーの電磁誘導の法則
誘電起電力をVとすると、Vは磁束\(\Phi\)の時間変化によって生じるので、
$$V=|\frac{d\Phi}{dt}|$$と書ける
今回のように、磁束の増減の方向がわからない場合には、レンツの法則を内包したファラデーの法則を使います!
ファラデーの法則(レンツの法則を内包)
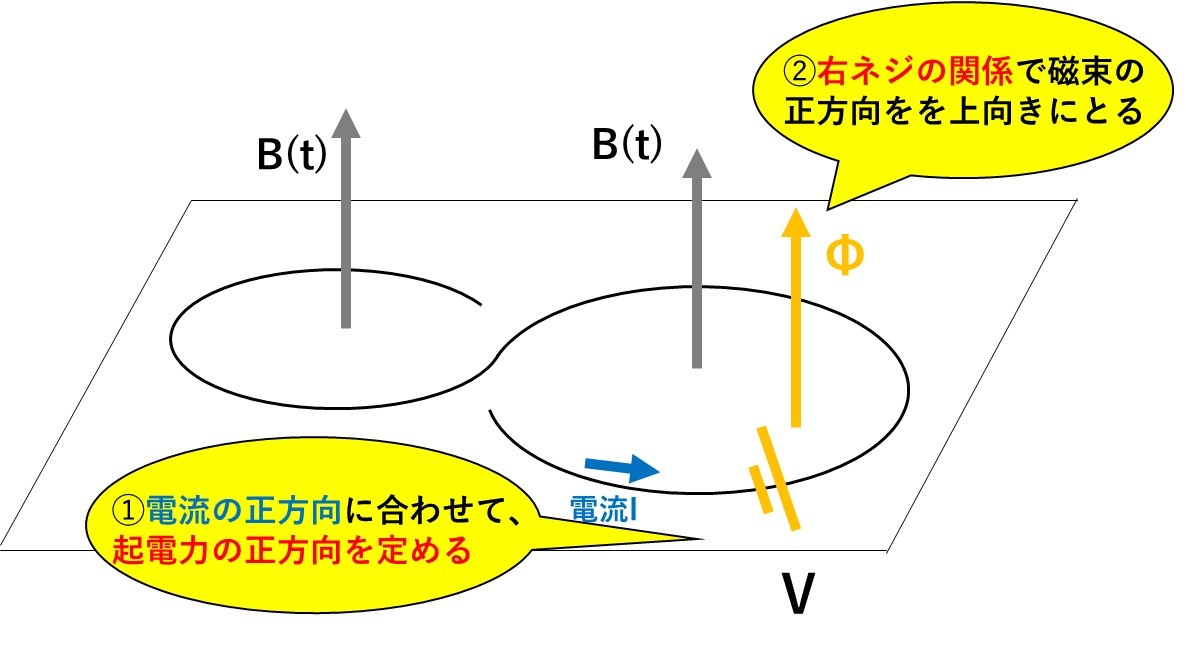
図のように、\(\Phi,V\)の正方向を連動させて決めるとき(右ネジの関係)、$$V=-\frac{d\Phi}{dt}$$と書ける
この方法を使うと、\(\Phi\)が増えるのか、減るのかわからなくても、答えを出すことができます!

この形、教科書で見たことありますが、こうやって使うのですね!
確かに、教科書に公式は書いてあるけど、参考書であっても使い方が書いていないことが多いから、しっかりここで勉強していこう!

解き方:ファラデーの法則を用いた例題
例題

紙面上に金属線が、図のようにねじれた形で置いてある。金属線の表面は絶縁体の被膜でおおわれており、全体の抵抗値はRである。鉛直上向きに一様な磁束密度\(B(t)=ksin(wt)+B_0\)の形で時間変化する磁場を加えた。この時、コイルに流れる電流を求めよ。ただし、電流の向きは、図の方向を正方向とする。
問題の進め方
➀右ネジの関係になるように、磁束と誘電起電力の正方向を決める。
➁➀で決めた軸の方向を見ながら、コイルを貫く全磁束を求める。
➂レンツの法則を内包したファラデーの法則の公式に代入する。
➀右ネジの関係になるように、磁束と誘電起電力の正方向を決める。
まずは、図のように、磁束と誘電起電力の正方向を決めます!

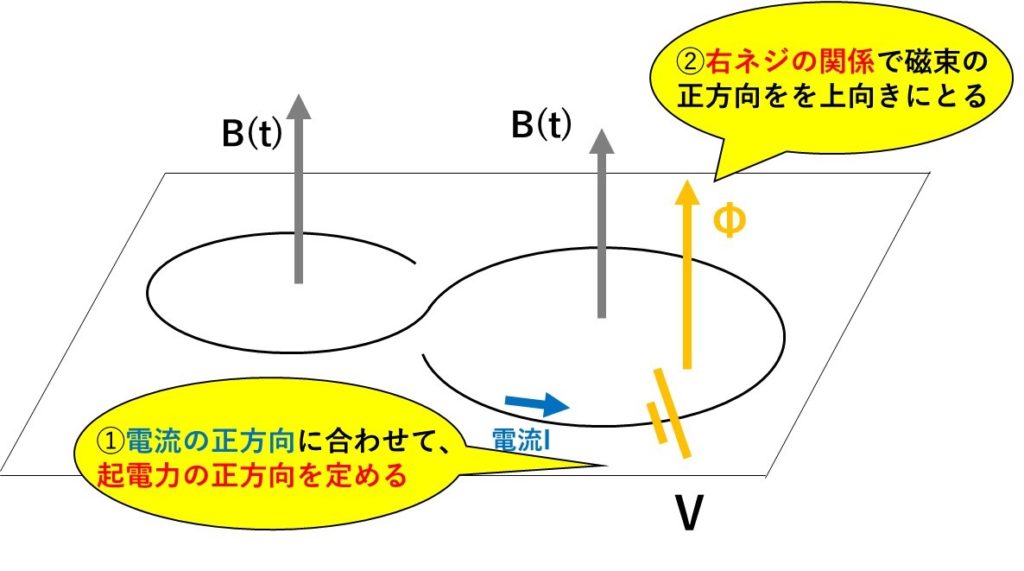
今回、電流の正方向の向きが決まっているので、電流の向きと起電力の正方向を一緒にしておきます!
このあとは、もう一つコイルのループがあるので、そっちの正方向も考えていきます。

さっきと同じように、電流の正方向と起電力の正方向を、同じ向きで決めればOKです!
➁➀で決めた軸の方向を見ながら、コイルを貫く全磁束を求める。

次は、図を見ながらコイルを貫く全磁束を求めていきます!
軸と同じ方向をプラス、軸と逆向きをマイナスとすると、全磁束\(\Phi\)は、
$$(全磁束\Phi)=+B(t)S_2-B(t)S_1$$$$=(S_2-S_1)B(t)$$$$=(S_2-S_1)\{ksin(wt)+B_0\}(問題文のB(t)を代入)$$
磁束密度Bから磁束\(\Phi\)を出すには、面積を掛けなくちゃいけないことを忘れずに!

➂レンツの法則を内包したファラデーの法則の公式に代入する。
ファラデーの法則(レンツの法則を内包)

図のように、\(\Phi,V\)の正方向を連動させて決めるとき(右ネジの関係)、$$V=-\frac{d\Phi}{dt}$$と書ける
ここまで来たら、上の公式に➁で求めた、全磁束を代入して起電力を求めていくだけです!
$$V=-\frac{d\Phi}{dt}$$$$=-\frac{d}{dt}\{(S_2-S_1)ksin(wt)+B_0(S_2-S_1)\}$$$$=-k(S_2-S_1)\frac{d}{dt}sin(wt)+0 ※B_0(S_2-S_1)は定数⇨微分したら0$$$$=wk(S_1-S_2)coswt$$
$$\therefore V=wk(S_1-S_2)coswt$$となります!
最後に、回路方程式を立てるだけです!

回路全体の抵抗を一部分に集約し、誘電起電力も一か所に集めると、上のようになります。
図をみて、回路方程式を立てると、
$$V=RI$$$$I=\frac{V}{R}$$$$V=wk(S_1-S_2)coswtを代入して$$
$$\therefore I=\frac{wk(S_1-S_2)}{R}coswt・・・(答え)$$
まとめ:難関大の問題はレンツの法則を内包した形で解く!
今回は、コイルを貫く磁束が時間変化するときに、どういう風に解けばよいか説明しました!
このような場合は、レンツの法則を内包したファラデーの法則を使えばよいのでした。
ファラデーの法則(レンツの法則を内包)

図のように、\(\Phi,V\)の正方向を連動させて決めるとき(右ネジの関係)、$$V=-\frac{d\Phi}{dt}$$と書ける
➀右ネジの関係になるように、磁束と誘電起電力の正方向を決める。
➁➀で決めた軸の方向を見ながら、コイルを貫く全磁束を求める。
➂レンツの法則を内包したファラデーの法則の公式に代入する。
この式の立て方は、参考書に載っていることが非常に少ないので、塾や予備校に通っている人と差がつきやすい場所でもあります!
そして、このやり方は、磁束が時間変化する場合はもちろん、時間変化しない場合でも解くことができるので、自分の持っている問題集で練習しましょう。
今回は以上です。
関連記事自己誘導・相互誘導とは?インダクタンスの導出を例題とともにわかりやすく解説


