
自己誘導と相互誘導って何ですか?
コイル(導線)は、自分の中を貫く磁束の変化を、とてつもなく嫌うのでした。
嫌いなのにも関わらず、自分で磁束の変化を起こしてしまう、おっちょこちょい者なのが、自己誘導で、相方のおっちょこちょいにいつも巻き添えを食らうのが、相互誘導です
今回は、そんな自己誘導・相互誘導の話をしていきます。
この記事を読めば、『自己・相互インダクタンスの導出』ができますので、最後まで見ていきましょう!
前回の記事は【難関大必須】ファラデーの法則を完全理解【問題の解き方を徹底解説】を参考にどうぞ。
目次
コイルの自己誘導・相互誘導は漫才コンビ

自己誘導・相互誘導が漫才コンビってどういうことですか?
まずは、自己誘導から説明していきます!
その①:自己誘導はおっちょこちょい!

コイルに電流を流すと、右ネジが回る方向に対して、磁場が発生しました!
その大きさは、単位長さ当たりのコイルの巻き数をnとした時に$$H=nI$$と書けましたね。
つまり、コイルに電流が流れると、自分自身で磁場を作ります。

もともと磁場がなかったところに、コイルが自分で磁場を変化させると、どうなるかな?


あ!変化を妨げる方向に電磁誘導が起こりました!

コイルは、環境の変化を嫌うので、直前の環境(磁場が0の状態)に戻そうと、自分で磁場を作り出します!
このように、『やっぱ前の環境がいい!』と言って、自分で作り出した磁場を、電磁誘導で消そうとすることを、自己誘導といいます。
自分で増やした磁場を、すぐ消そうとするなんて、おっちょこちょいにもほどがあるね。

自己誘導
➀コイルに電流を流す
➁電流に対して右ネジの方向に磁場が発生
➂磁束の変化を妨げる向きに磁場が発生(レンツの法則)
その②:相互誘導は相方の巻き添え

相方の巻き添えって何ですか?
さっきのおっちょこちょい者の隣にいた、もう一人のコイル君も、実は被害を受けているんだ!


ただ隣にいた『コイル2』も、コイル1が作り出した磁場を受けて環境が変化してしました。
もちろん、コイルは環境の変化が嫌いなので、コイル2は『マジやめてくれ!』というわけですね!

相方の巻き添えを食らったコイル2も、すかさず磁場の変化を妨げる向きに、磁場を作り出して相方の出した磁場を減らすのです。
このように、自分は何もしていないのにも関わらず、相方のせいで自分も磁場を作ることを、相互誘導といいます。

相互誘導、かわいそうすぎます・・
相互誘導
➀自己誘導コイルが磁場を作り出す
➁➀が隣にいただけのコイルの環境を変える
➂何もしてないコイルも、磁場の変化を妨げる向きに磁場を作る
つまり、自己誘導と相互誘導はセットで、自己誘導はおっちょこちょい、相互誘導は相方の巻き添えを食らうと覚えておきましょう!
自己誘導・相互誘導による誘電起電力の大きさ

自己誘導・相互誘導ともに、電磁誘導を起こして、自分自身のコイル内の磁場の変化を妨げる向きに、磁場を作るのでした。
それでは、どれくらいの誘電起電力が発生するのか、例題とともに見ていきましょう。
この問題は、入試問題としても出題されるし、電磁誘導の練習にもなるから、紙とペンを用意してしっかり練習しよう!

例題
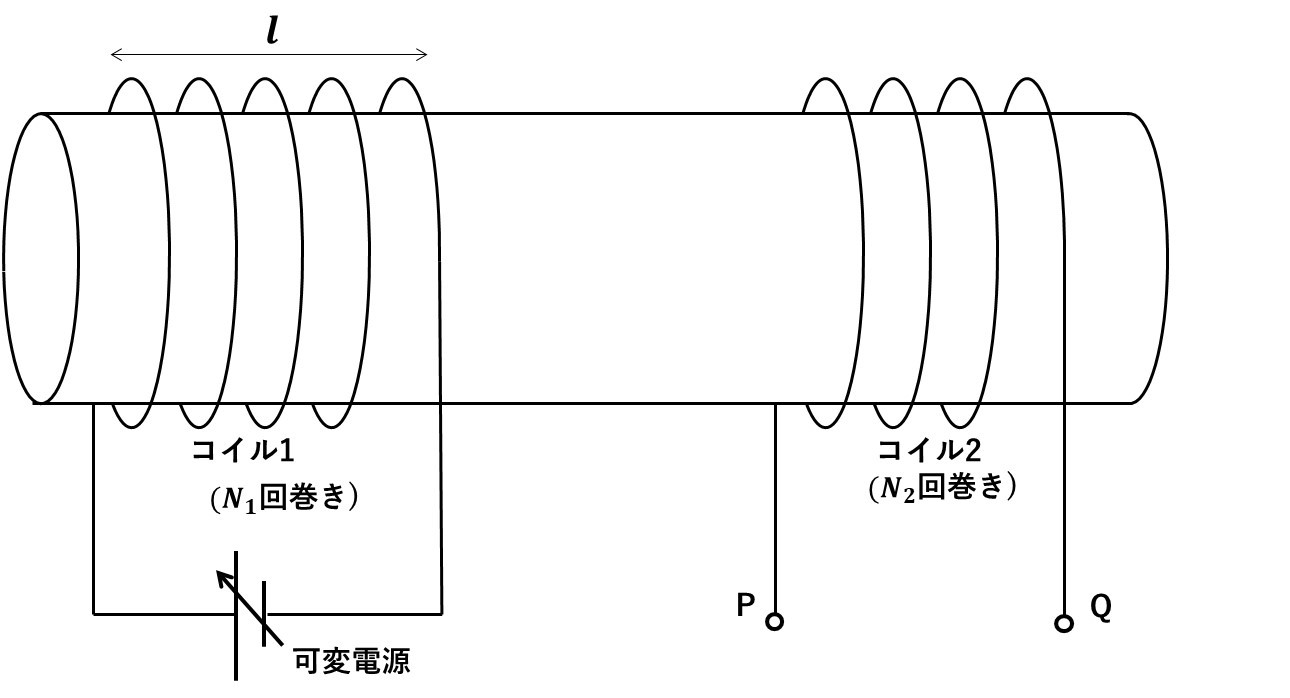
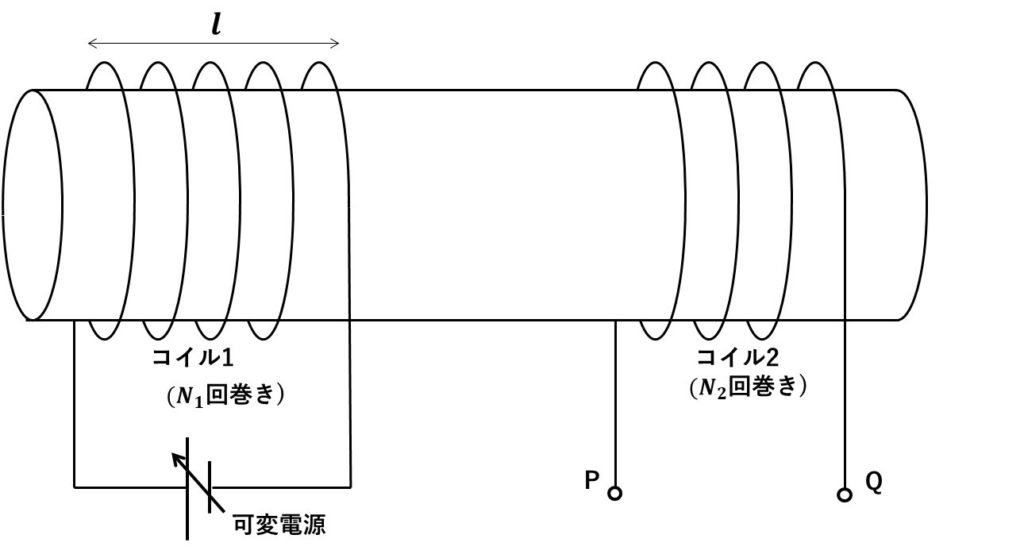
断面積S、透磁率\(\mu\)の鉄心に図のように2つのコイルがまかれている。コイル1に流れる電流を\(I\)とするとき、以下の問いに答えよ。
(1)鉄心内の磁束密度を求めよ。
次に電流\(I\)を時間\(\Delta t\)の間に\(\Delta I\)だけ変化させた。
(2)コイル1に生じる誘電起電力\(V_1\)を求めよ。ただし、左側の回路に時計回りに電流を流そうとする向きを\(V_1\)の正方向とする。
(3)コイル2に生じる誘電起電力\(V_2\)を求めよ。ただしPからQに向かう方向を正方向とする。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
問題の解答:自己誘導相互誘導
考え方
(1)ソレノイドコイルの作る磁場から求める。
(2)電磁誘導の正方向を定めて、コイルを貫く全磁束から誘電起電力を求める。
(3)(2)と同様にして、相互誘導による誘電起電力を求める。
(1)の解答
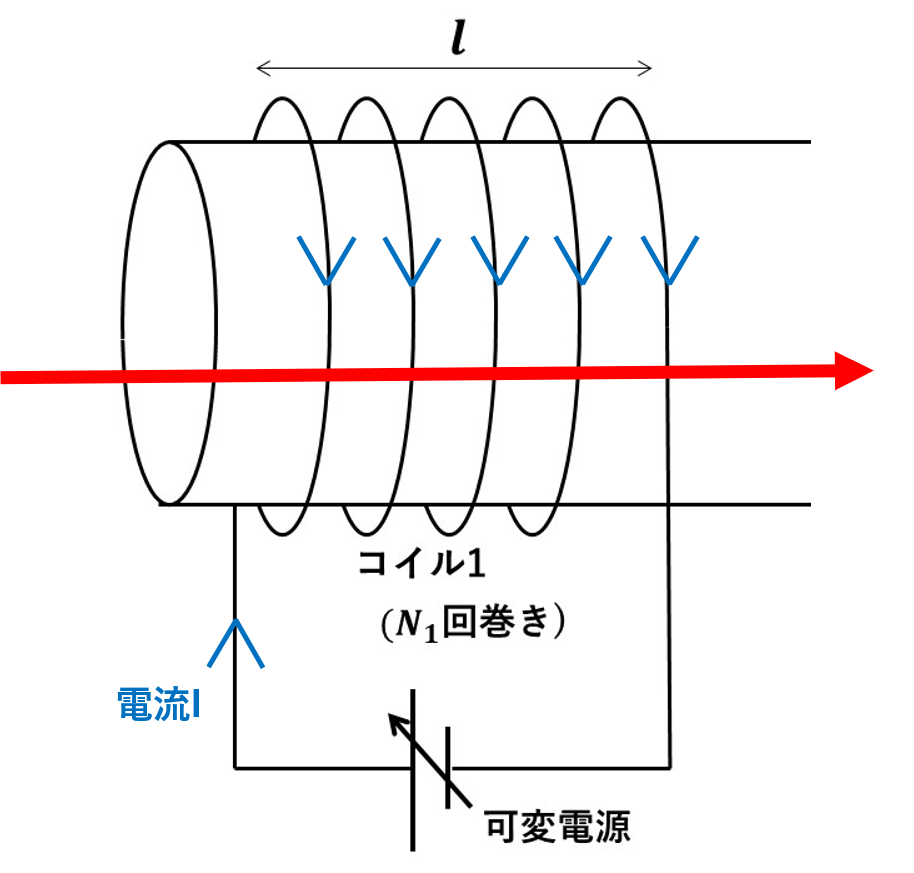
ソレノイドコイルに電流を流すと、右ネジが回る方向に対して、磁場が発生しました!
その大きさは、単位長さ当たりのコイルの巻き数をnとした時に$$H=nI$$と書けましたので、単位長さ当たりの巻き数\(n=\frac{N_1}{l}\)であることに注意して、
$$B=\mu H$$$$=\mu \frac{N_1}{l}I・・・(答え)$$
(2)の解答
例題

断面積S、透磁率\(\mu\)の鉄心に図のように2つのコイルがまかれている。コイル1に流れる電流を\(I\)とするとき、以下の問いに答えよ。
次に電流\(I\)を時間\(\Delta t\)の間に\(\Delta I\)だけ変化させた。
(2)コイル1に生じる誘電起電力\(V_1\)を求めよ。ただし、左側の回路に時計回りに電流を流そうとする向きを\(V_1\)の正方向とする。
電磁誘導が起こりますので、まずは磁束と誘電起電力の正方向を、右ネジの関係で決めましょう!

※磁束と誘電起電力の正方向を、右ネジの関係で決めるやり方を知らない人は、【ファラデーの法則の完全版!高校物理の電磁誘導を徹底解説【難関大に対応!!】】をご覧ください。

今回は、問題文に『時計回りに電流を流そうとする向きを起電力の正方向とする』とあるため、\(V_1\)を図の向きに決めてから、磁束の正方向を右ネジの関係になるように決めました。
コイル1が作る全磁束は、$$\Phi_1=+BS×N_1となります。$$$$(プラスは、磁束正方向と同じ向きだから)$$
\(+BS\)は、単位長さ当たりが作る磁束なので、コイル1が作る全磁束は、\(N_1\)倍しなくてはいけないことに注意です。
(1)の答え$$B=\mu \frac{N_1}{l}Iを代入して$$$$\Phi_1=+BS×N_1$$$$=\frac{\mu {N_1}^2S}{l}I$$
ファラデーの法則に、上で求めた全磁束を代入すると、$$\therefore V_1=-\frac{d\Phi_1}{dt}$$$$=-\frac{\mu {N_1}^2S}{l}×\frac{dI}{dt}$$$$=-L\frac{dI}{dt}・・・(答え)$$
答えの中にある\(L\)は自己インダクタンス [H:ヘンリー]という定数だよ!

自己誘導
$$V=-L\frac{dI}{dt}$$$$自己インダクタンスL=\frac{\mu {N_1}^2S}{l}$$$$[単位H:ヘンリー]$$
(3)の解答
例題

断面積S、透磁率\(\mu\)の鉄心に図のように2つのコイルがまかれている。コイル1に流れる電流を\(I\)とするとき、以下の問いに答えよ。
次に電流\(I\)を時間\(\Delta t\)の間に\(\Delta I\)だけ変化させた。
(3)コイル2に生じる誘電起電力\(V_2\)を求めよ。ただしPからQに向かう方向を正方向とする。

(3)は、問題文に『PからQの向きを起電力の正方向とする』とあるため、\(V_2\)を図の向きに決めてから、磁束の正方向を右ネジの関係になるように決めました。
コイル2が作り出す全磁束は、$$\Phi_2=+BS×N_2です。$$$$(プラスは、磁束正方向と同じ向きだから)$$
\(+BS\)は、単位長さ当たりが作る磁束なので、コイル2が作る全磁束は、\(N_2\)倍しなくてはいけないことに注意です。
(1)の答え$$B=\mu \frac{N_1}{l}Iを代入して$$$$\Phi_2=+BS×N_2$$$$=\frac{\mu N_1 N_2 S}{l}I$$
ファラデーの法則に、上で求めた全磁束を代入すると、$$\therefore V_2=-\frac{d\Phi_2}{dt}$$$$=-\frac{\mu N_1 N_2 S}{l}×\frac{dI}{dt}$$$$=-M\frac{dI}{dt}・・・(答え)$$
答えの中にある\(M\)は相互インダクタンス [H:ヘンリー]という定数だよ!

相互誘導
$$V=-M\frac{dI}{dt}$$$$相互インダクタンスL=\frac{\mu N_1 N_2S}{l}$$$$[単位H:ヘンリー]$$
まとめ:自己誘導・相互誘導は自分で導出できるようにしよう!

今回は、自己誘導・相互誘導について詳しく紹介しました!
この範囲は、電磁誘導と絡んで苦手な人が増えてきますが、しっかり導出できればそんなに難しくはありません。
何度も手を動かして、何も見なくても描けるようになるまで練習しておきましょう!
今回は以上です。
関連記事【簡単】電気振動の解き方をわかりやすく解説【結論:単振動と同じです】

