
・単振動の問題が解けません。
・何から手を付けていいかわからない。
今回は、上のような悩みを解決していきます。
単振動の問題って、大学入試において毎年頻出なのですが、解けない人がかなり多い分野でもあります。
苦手な原因は、ずばり『公式を暗記している』『何から手を付けたらいいかわからない』この2つです!
そこで、今回は例題とともに、単振動の問題の解き方を見ていこうと思います。
目次
【復習】単振動は等速円運動を横からみたもの

【単振動は等速円運動と変わらない!単振動の公式をわかりやすく導出してみた】の記事で、単振動は等速円運動を横からみた往復運動ということを勉強しました。
『だからなんやねん』と思う人もいるかと思いますが、導出や問題を解くうえで使う場面があるので、しっかり覚えておきましょう。
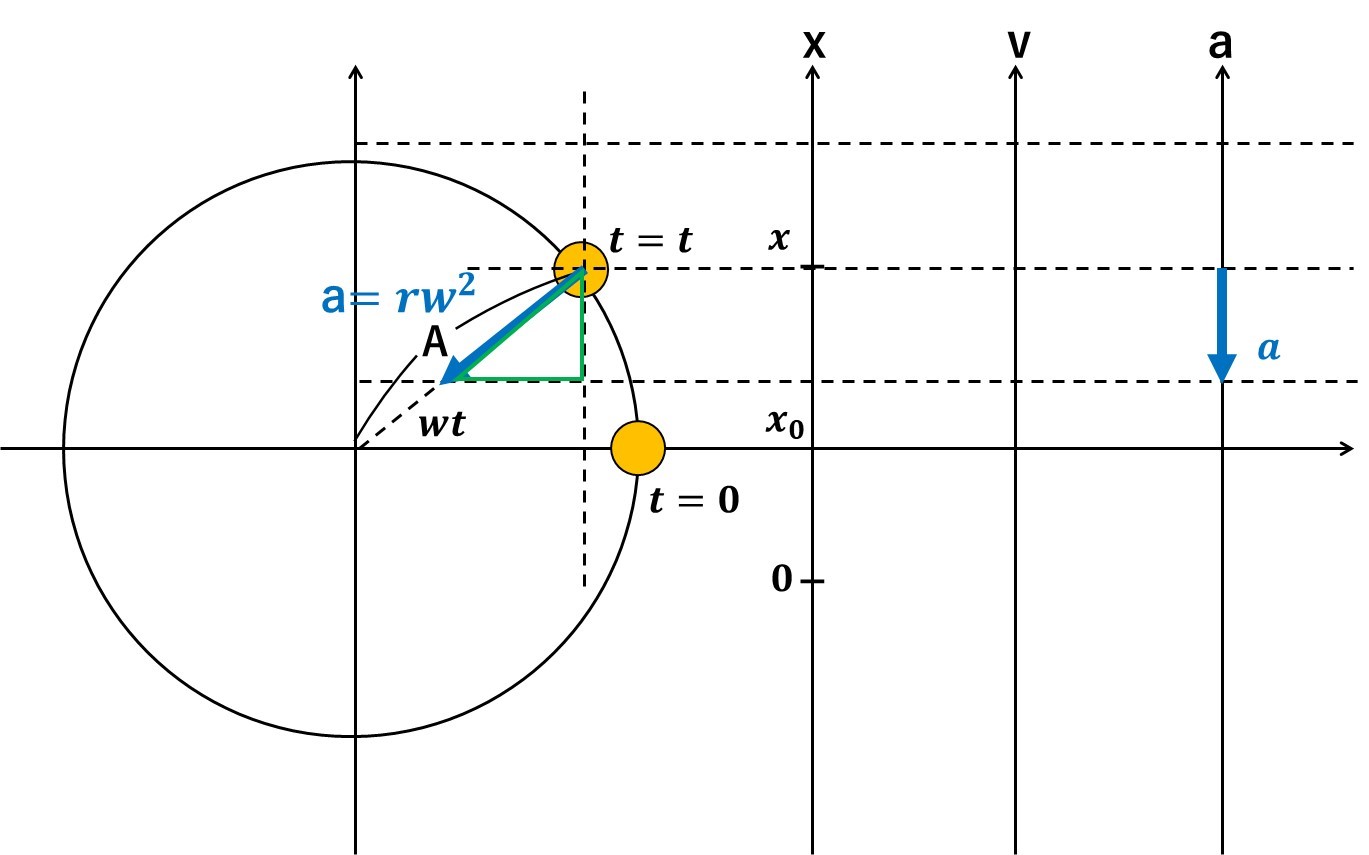
そして、この図から、単振動の加速度は$$a=-w^2(x-x_0)$$と求められました。
単振動の加速度
単振動の加速度は、\(角振動数をw、振動中心をx_0\)とした時、
$$a=-w^2(x-x_0)$$
単振動の問題を解く手順は2ステップ!

単振動の問題の解く手順は、以下の2ステップです!
単振動のポイント
➀まず、任意の位置\(x\)における運動方程式を立てる!
➁必ず\(x\)軸と同じ向きに加速度の正方向をとる!
どうして、\(x\)軸と同じ向きに加速度の正方向をとらなくちゃいけないかについても、前回やったね!

では、本当にこの方法で問題が解けるのか、例題を使ってみていきましょう。
例題:単振動の問題
例題
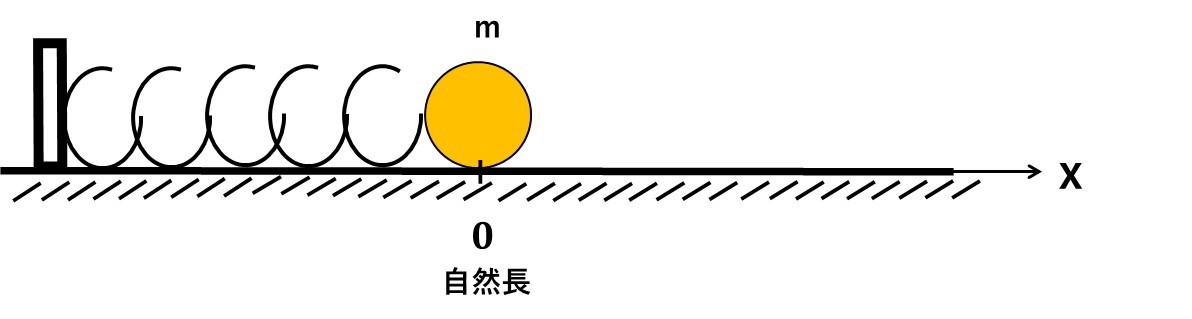
なめらかな水平面において、ばね定数kのばねを壁に固定し、他端に質量mの球をつなぐ。自然長を原点として、図のようにx軸をとり、時刻t=においてx=Aから球を静かに放すと、球は単振動し始めた。
(1)角振動数w、周期T、振動中心をもとめよ。
(2)速さの最大値を求めよ。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは、解説していくよ!

(1)の解答【単振動の角振動数w,周期T,振動中心】
例題

なめらかな水平面において、ばね定数kのばねを壁に固定し、他単に質量mの球をつなぐ。自然長を原点として、図のyぷにx軸をとり、時刻t=においてx=Aから球を静かに放すと、球は単振動し始めた。
(1)角振動数w、周期T、振動中心をもとめよ。
(2)速さの最大値を求めよ。
単振動のポイント
➀まず、任意の位置\(x\)における運動方程式を立てる!
➁必ず\(x\)軸と同じ向きに加速度の正方向をとる!
➀まず、任意の位置\(x\)における運動方程式を立てる!
まずは、図を見ながら、任意の場所における運動方程式を立てます!そのためには、力を描かなくてはいけないので、物体にかかる力を図示していきます。
ばねから受ける力は、以下のように表せます。
ばねによる弾性力
・【大きさ】\(k\)×(自然長からの変位)※変位は今ある位置と自然長の位置の(大-小)
・【向き】自然長方向

ひとつ質問なのですが、『任意の位置』の決め方って自然長より長くても短くても、どっちでもいいってことですか?
いい質問だね!答えはどっちでもOKなんだ!

➁必ず\(x\)軸と同じ向きに加速度の正方向をとる!

上の考えを踏まえて、➀自然長よりも長い場合➁自然長よりも短い場合、の2パターンでばねによる弾性力を描いてみると、上のようになります。
加速度aの正方向をx軸正方向と同じ向きにとって、2パターンともに運動方程式を書いてみると、
$$【自然長よりも長い場合】ma=-k(x-0)$$
$$【自然長よりも短い場合】ma=k(0-x)$$$$=-k(x-0)$$

あ!式が同じになりました!
これで、どこを任意の位置にとっても、式が同じになることがわかったね!

運動方程式は$$ma=-k(x-0)$$と書けたので、加速度aは
$$\therefore a=\frac{k}{m}(x-0)$$
と書けます。ここまで来たら、単振動の加速度の式と見比べます。
単振動の加速度
単振動の加速度は、\(角振動数をw、振動中心をx_0\)とした時、
$$a=-w^2(x-x_0)$$
$$a=\frac{k}{m}(x-0)$$$$a=-w^2(x-x_0)$$
これらを比較すると、$$w=\sqrt\frac{k}{m}$$$$振動中心x=x_0=0$$
\(T=\frac{2\pi}{w}\)を利用して、
$$T=\frac{2\pi}{w}=2\pi\sqrt\frac{m}{k}$$
となり、(1)の答えがでました。
(2)の解答【速さの最大値】
例題

なめらかな水平面において、ばね定数kのばねを壁に固定し、他単に質量mの球をつなぐ。自然長を原点として、図のyぷにx軸をとり、時刻t=においてx=Aから球を静かに放すと、球は単振動し始めた。
(1)角振動数w、周期T、振動中心をもとめよ。
(2)速さの最大値を求めよ。

速さが最大になるところってどこなの?
まずは、単振動の図をみて確認してみよう!


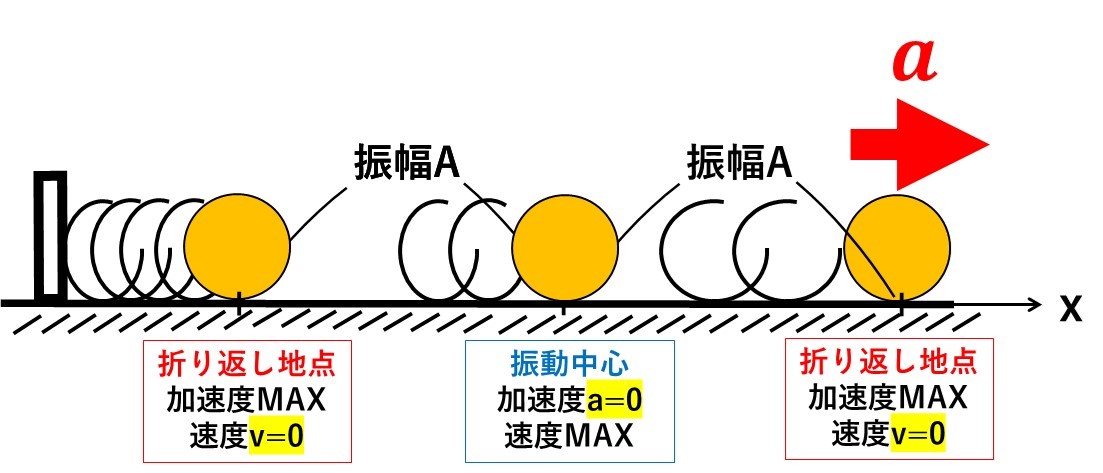
放した地点と振動中心の間の距離のことを振幅といい、摩擦がない単振動では2つの振幅が必ず同じになります。
折り返し地点では、一度止まるので速度は0になり、急激に引っ張られるので加速度は最大になります。
一方振動中心では、速度が最大になり、加速度は0になります。

今回は、速さが最大になるときの大きさを求めるので、折り返し地点での速さですね!
2点間の距離が与えられたときは、力学的エネルギー保存則、あるいはエネルギー保存則を使うのでした。

(1)より、振動中心は原点、振幅は問題文よりAとわかるので、力学的エネルギー保存の法則から
$$\frac{1}{2}kA^2=\frac{1}{2}m{v_{max}}^2$$
$$\therefore v_{max}=A\sqrt\frac{k}{m}$$
となります。
まとめ:単振動の問題は解き方を覚えれば簡単です

今回は、単振動の基本について、例題を通して勉強してきました。
単振動の周期などの公式を丸暗記していた人や、単振動の問題の解き方を知らなかった人は、今回の内容で克服できたのではないでしょうか。
次の記事では、物理のエッセンスにも詳しく載っていない、単振動と等速円運動をリンクさせた解き方について紹介していきます!

