重心を求める公式を覚えるな！【くり抜いた円盤の解き方をわかりやすく解説】

悩んでる人

・重心ってそもそも何？
・公式が複雑でわからない
・問題はどーやって解けばいいの？

今回は、こんな悩みを解決していきます！

そして、最後には以下の例題を解けるようにしていきます。

例題

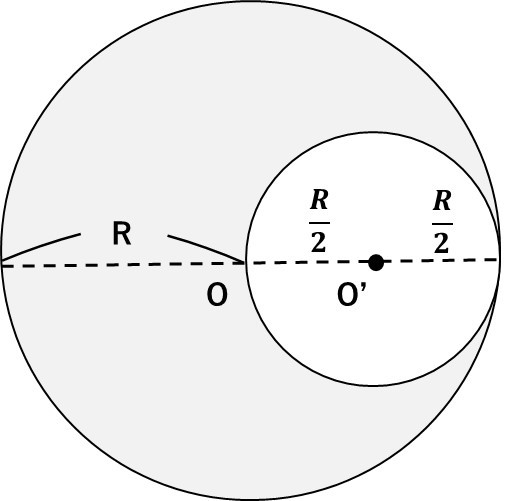
半径2Rの円盤から、図のように半径\(\frac{R}{2}\)の円盤をくりぬいた。この時、残った円盤の重心の位置を答えよ。

【基礎を理解】そもそも重心は全重力の作用点のこと

重心とは、全質量がそこに集中しているとみなせる点です。

つまり、物体にかかる全重力の作用点ということができます！

例えば、質量Mとmの物体を、質量が無視できる棒でつなぐと下のようになるよ！

塾長

また、重心の特徴として、重心では『力のモーメント』がつり合います！

力のモーメントは、$$力F×支点から力Fの作用線までの距離l$$

で求めることができました。

重心を支点とした、重力モーメントは必ずつり合うことから、全体の重心は、各物体の重心の位置を、質量の逆比に内分する点、ということがわかります！

確かに、上の絵で重心を支点にした、力のモーメントはつり合います！

重心を支点とした時の力のモーメントが、必ずつり合うことを覚えておけば、重心の公式を覚える必要はないね！

塾長

例題：くり抜いた円盤の問題

問題に入る前に、軽く練習しておこう！

塾長

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

問題の解答

上の図のように、縦横それぞれを1つの物体としてみて、それぞれの重心を結んで、長さの逆比で内分すればOKだよ！

塾長

悩んでる人

全体の重心が、物体の上にないのですが、それでもいいのですか？

対称的でない図形の場合、全体の重心は物体の上にないことが多いから、気にしなくても大丈夫だよ！

塾長

問題の解答：くり抜いた円盤の重心を求める

例題

半径2Rの円盤から、図のように半径\(\frac{R}{2}\)の円盤をくりぬいた。この時、残った円盤の重心の位置を答えよ。

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

それでは解説していくよ！

塾長

まずは、重心を求めるために、各物体の質量比を求めていくが、物体の密度は同じなので、今回は面積比がそのまま質量比になります。

抜け落ちた部分の面積

抜け落ちた部分の面積は、半径\(\frac{R}{2}\)なので、

$$\pi (\frac{R}{2})^2$$$$=\frac{\pi}{4}R^2$$

となります。

残りの円の面積

灰色の面積は、半径Rの円の面積から、半径\(\frac{R}{2}\)の円の面積を引いたものになるので、

$$\pi R^2-\pi (\frac{R}{2})^2$$$$=\frac{3}{4}\pi R^2$$

となります。

よって、2つの物体の質量比（面積比）は、\(\frac{\pi}{4}R^2と\frac{3}{4}\pi R^2\)で1:3となります！

質量比がでたから、あとはそれぞれの重心を結んで、質量の逆比で内分だね！

塾長

この3つを図に描き込んで、質量比が全体の重心になるように書くと、上のようになります！

求めたい場所は、抜け落ちて残った部分の重心の位置なので、中心から\(G_2\)の距離を\(x\)とすると、

$$x:\frac{R}{2}=1:3$$$$x=\frac{R}{6}$$

と求めることができます。

なので、中心から\(\frac{R}{6}\)の点が答えになります。

まとめ：重心の問題の解き方は簡単！

今回は、重心の定義とその問題の解き方について話してきました。

大切な内容をまとめると、以下のようになります。

くれぐれも、重心の公式を教科書や、参考書に載っているような形で、覚えないようにしてください。

自分の持っている問題集で練習して、重心問題は完璧にできるようにしておきましょう！