
・弾性力の大きさってどうやって求めればいいの?
・ばねの問題が苦手
・弾性力の向きがイマイチわからない
今回は、こんな悩みについて解決していきます。
簡単な問題だと解ける人が多い、ばねの問題ですが、ばねの両端に物体がついたり、ばねが2つついたりすると解けなくなる人が非常に多くなります。
今回の内容で、ばねの基本をしっかり押さえて、ばねの問題に強くなりましょう!
また、ばねに強くなるだけで、後から勉強する『単振動』にも強くなりますので、頑張っていきましょう。
弾性力はばねが自然長に戻ろうとする力!

弾性力とは、ばねが自然長の長さに戻ろうとする力のことで、その大きさは自然長からの変位\(x\)に比例し、
$$F=kx(k:ばね定数)$$と表すことができます。
そして、弾性力の向きは、必ず自然長の長さに戻ろうとする方向に働きます!
ポイント
$$【力の大きさ】F=kx(k:ばね定数)$$$$【向き】自然長に戻ろうとする方向$$
早速、問題を解いて練習していこう!

例題:ばね問題の解き方
例題
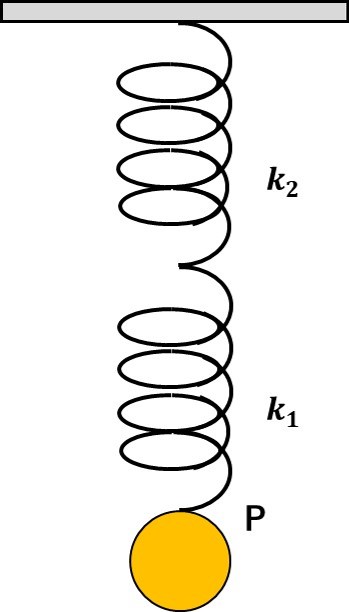
ばね定数が\(k_1,k_2\)の2つのばねをつなぎ、質量mのおもりPをつるして静止させた。
(1)\(k_1\)のばねの伸び\(x_1\)を求めよ。
(2)\(k_2\)のばねの伸び\(x_2\)を求めよ。
(3)2つのばねを1本のばねと見た時のばね定数\(k_t\)を求めよ。
(物理のエッセンスより引用)
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは解説していくよ!

(1)の解答
例題

ばね定数が\(k_1,k_2\)の2つのばねをつなぎ、質量mのおもりPをつるして静止させた。
(1)\(k_1\)のばねの伸び\(x_1\)を求めよ。
考え方
力の描き方は、以下の手順で書くのでしたね!
力の描き方
1.着目物体の数だけ図を描く!
2.場から受ける力(重力や静電気力)を描き込む!
3.他物体との接触点に印をつけ、そこを根本として、物体が受ける接触力のみを描く!
まずは、こんな感じで、図をいくつか書いてみましょう!
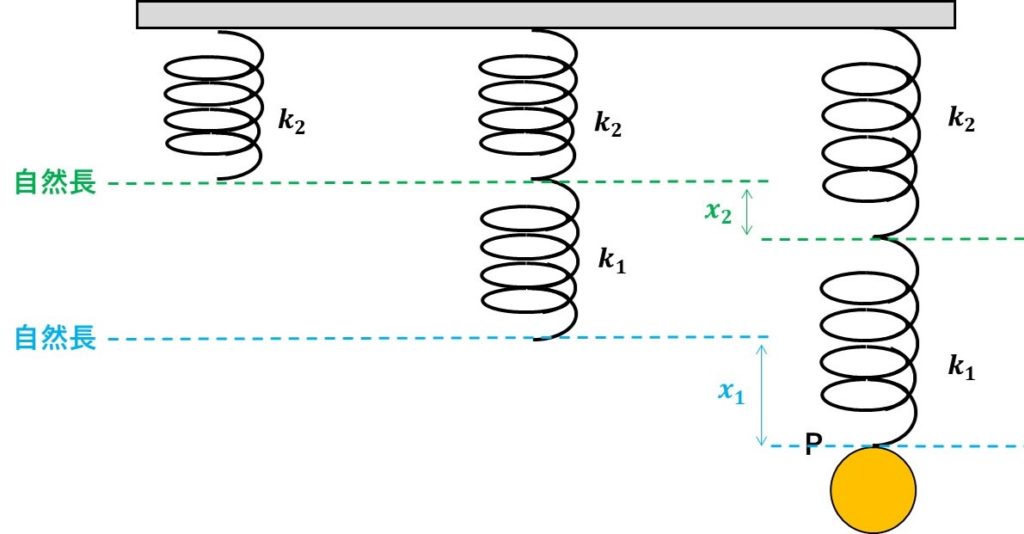
横並びで図を描くことで、自然長からの変位がわかりやすくなります!
まずは、この図に\(k_1\)のばねの力を描いていきます。ボールに働く力は、
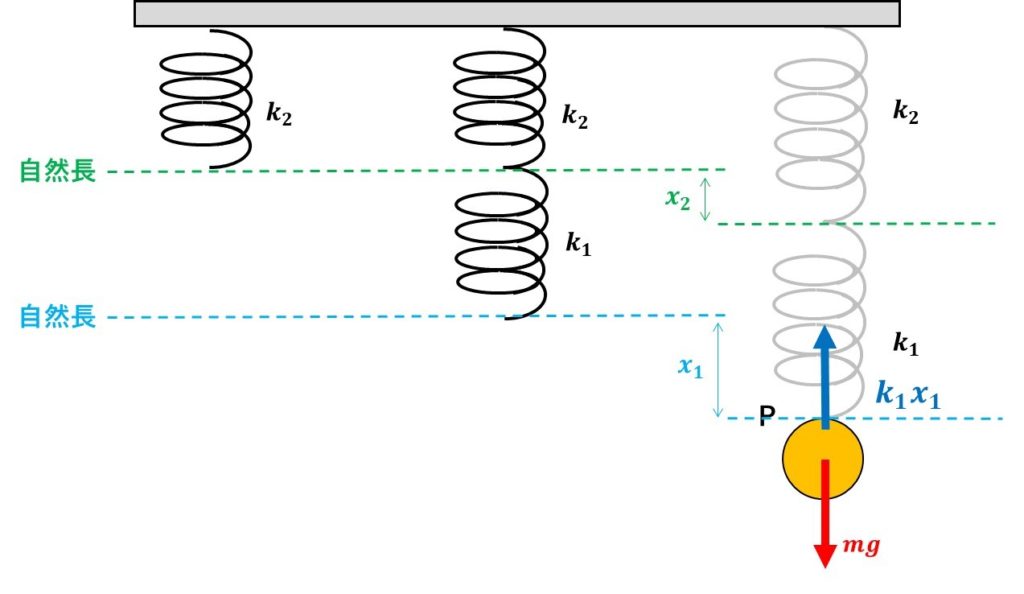
となります!(着目物体以外は、色を薄くしています。)
そして、物体は静止しているので、つり合いの式から
$$k_1x_1=mg$$$$\therefore x_1=\frac{mg}{k_1}$$
(2)の解答
例題

ばね定数が\(k_1,k_2\)の2つのばねをつなぎ、質量mのおもりPをつるして静止させた。
(2)\(k_2\)のばねの伸び\(x_2\)を求めよ。
上と同じように、力を描いていきます!
さっきは、ボールを着目物体にして力を描いてきましたが、次は\(k_1\)のばねに働く力を描いていきます。

着目物体が受ける力は、上のように描け、静止していることからつり合いの式を立てると、
$$k_2x_2=mg$$$$\therefore x_2=\frac{mg}{k_2}$$
となります。
(3)の解答
例題

ばね定数が\(k_1,k_2\)の2つのばねをつなぎ、質量mのおもりPをつるして静止させた。
(3)2つのばねを1本のばねと見た時のばね定数\(k_t\)を求めよ。
考え方!
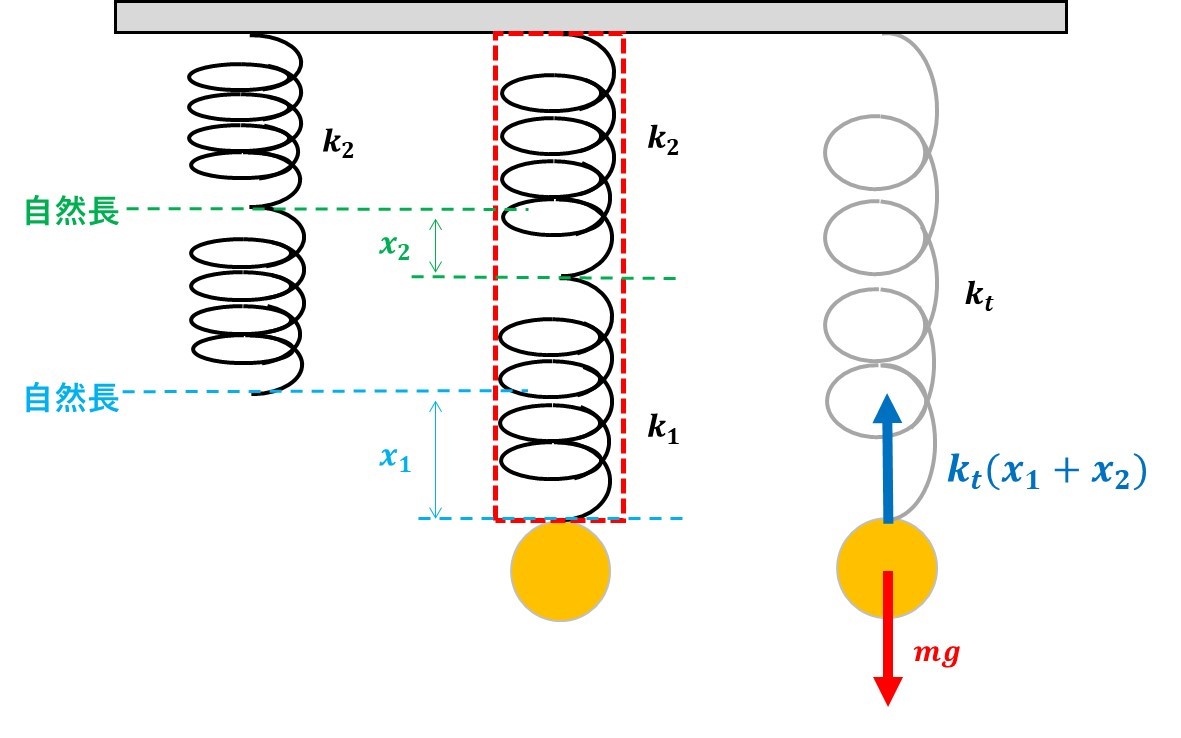
上のように2つのばねを1本とみると、合計で\((x_1+x_2)\)だけ伸びていることがわかります。
ボールにかかる力のつり合いの式を立てると、
$$k_t(x_1+x_2)=mg$$
(1)(2)の答え、\(x_1=\frac{mg}{k_1}x_2=\frac{mg}{k_2}\)を代入すると、
$$k_t(\frac{1}{k_1}+\frac{1}{k_2})=1$$$$\therefore k_t=\frac{k_1k_2}{k_1+k_2}$$
となります。
まとめ:ばねの問題を解くときはばねを分けて考える!

今回は、弾性力とばねの使い方について話してきました。
まとめておくと、以下のようになります。
ポイント
$$【力の大きさ】F=kx(k:ばね定数)$$$$【向き】自然長に戻ろうとする方向$$
\(x\)が自然長からの変位ということと、向きが必ず自然長方向になることの2つを覚えておけば、ばねの問題は間違えることがなくなります!
力をしっかり描けるようになることが、力学の問題で安定して点数をとるコツなので、しっかりと自分で力を描く練習をし置きましょう。


