
・運動量保存則って何?
・どういう時に公式が使えるの?
・運動量保存則の導出はどうするの?
今回は、上のような疑問を解決していきます!
この記事を読めば、運動量保存則の使い方がわかるので、力学全体の問題への理解が深まりますよ!
✔この記事の内容
・物理における系とは?
・運動量保存則の導出
・公式が使える条件
物理における系とはグループのこと!

運動量保存則について話していく前に、物理における『系』の話をしていきます。
系とは、簡単に言えば、グループみたいなものを言います。

例えば、学校のクラスの中でも、『〇〇ちゃんグループ』みたいに、普段一緒にいるグループがありますよね。
そんな感じで、物理でもたくさんのものを、ひとまとまりにして考えることを、物体系といいます。

なるほど!先生は、いつも一人ですよね、、
悲しいこと言わないでよ、、。そういうのは、物理では孤立系といいます。

ポイント
✔ 系・・・グループのこと
✔ 物体系・・・いくつかの物体をグループとして、まとめてみること
さらに、仲良しグループの中でも喧嘩したり、あるいはグループ外とも、もめたりするよね。
物理では、グループ内の物体間で働く力のことを内力、グループ外からかかってくる力のことを外力といいます。
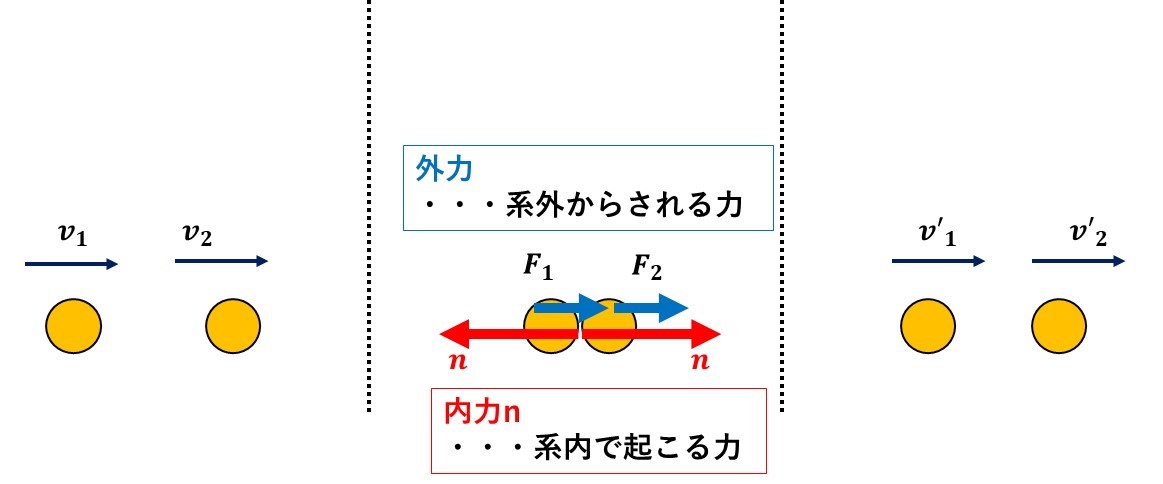
内力・外力は非常に大切なので、よく覚えておこう!
運動量保存則の導出の証明

それでは、さっそく運動量保存則の導出をしていきましょう。
導出、というと身構えてしまう人がたくさんいますが、今回はそんなに難しくないので、できるようにしておきましょうね!
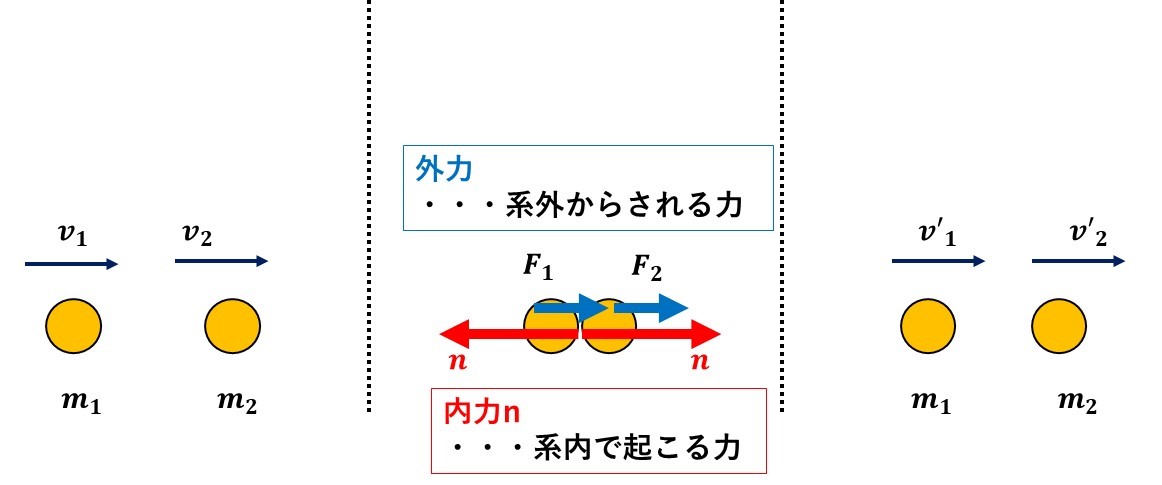
まずは、2つの物体それぞれの運動量と力積の関係の式を、立てていきます!
運動量と力積の関係の式は、『左辺に、運動量変化』、『右辺に、力がどのくらいかかったか』を書けばいいので、
$$m_1\vec{{v_1}'}-m_1\vec{v_1}=F_1\Delta t-n\Delta t$$$$m_2\vec{{v_2}'}-m_2\vec{v_2}=F_2\Delta t+n\Delta t$$
となります。
今、2つの物体それぞれについて考えましたが、2つを1つの系として考えます。
2つを1つとして見るから、式も足し算して考えればOKだよ!

$$m_1\vec{{v_1}'}-m_1\vec{v_1}=F_1\Delta t-n\Delta t$$$$m_2\vec{{v_2}'}-m_2\vec{v_2}=F_2\Delta t+n\Delta t$$
これを足して整理すると、
$$(m_1\vec{{v_1}'}+m_2\vec{{v_2}'})-(m_1\vec{{v_1}}+m_2\vec{{v_2}})=(F_1+F_2)\Delta t$$
となります。
式をみると、系全体の運動量は、外力の力積によって変化していることがわかります。
さらに、外力0(F=0)のとき、つまり内力のみのときは、右辺が0になるので、系全体の運動量は保存することがわかりますね!
運動量保存則
物体系に働く外力が0(内力のみ)のときには、運動量が保存する
$$m_1\vec{{v_1}}+m_2\vec{{v_2}}=(一定)$$

運動量保存則って、何か身近な例とかありますか?
じゃあ、キャスター付きの、回るイスの上に座って、足を浮かせた状態で移動できるかな?


思いっきり前後しても、全く進みません、、
だよね!これは、いすと自分が『系』で、内力しか働かないから、初め静止していた状態からスタートすると、運動量が保存して動かないんだ。


なるほど!身近にも、運動量保存があるのですね!
まとめ:運動量保存が使える条件を理解しておこう!
今回は運動量保存則については話してきました!
内容をまとめると、以下のようになります。
ココがポイント
受験生が見落としがちな、運動量保存式の導出もやったので、理解を深めるためにも、自分で導出できるようにしておきましょう。


