交流回路をベクトルを使って解く方法を参考書よりもわかりやすく解説！！

悩んでる人

・交流問題の解き方がわからない
・参考書を見ても問題が解けない

私も高校生のときに、独学で交流回路の解き方について勉強していましたが、まったく解けずに、大学は不合格になりました。

浪人して物理の成績を伸ばした今言えることは、『交流回路ってやること直流回路と変わらないな』ってことです。

そこで今回は、参考書に書いてない交流問題の解き方について、今回はベクトルを使って解くやり方について、紹介していきます。

この記事を読めば、交流回路だけなく、直流回路の問題も得意にできるので、最後まで見ていってください。

交流回路の解き方はたった2つ！

交流回路の問題って、テクニックで解くみたいなのがありますが、そんなものは使い方を間違えてしまえば、満点どころか0点になってしまいます。

特に、物理のエッセンスは、テクニック的なことしか書いていないので、参考になりません。

それでは、どうやって解けばいいのか、解き方はたった2パターンしかありません。

解き方は、上の2通りあるのですが、前回は➀の微積の知識を使って解くやり方について、紹介ましたので、今回はベクトルを使ったやり方について、話していきます。

※前回の記事は【交流回路の解き方は2パターンだけ！RLC回路の例題とともにわかりやすく解説！！】を参照

それでは、前回と同じ例題で、並列交流回路の問題を解いていこう！

例題

例題

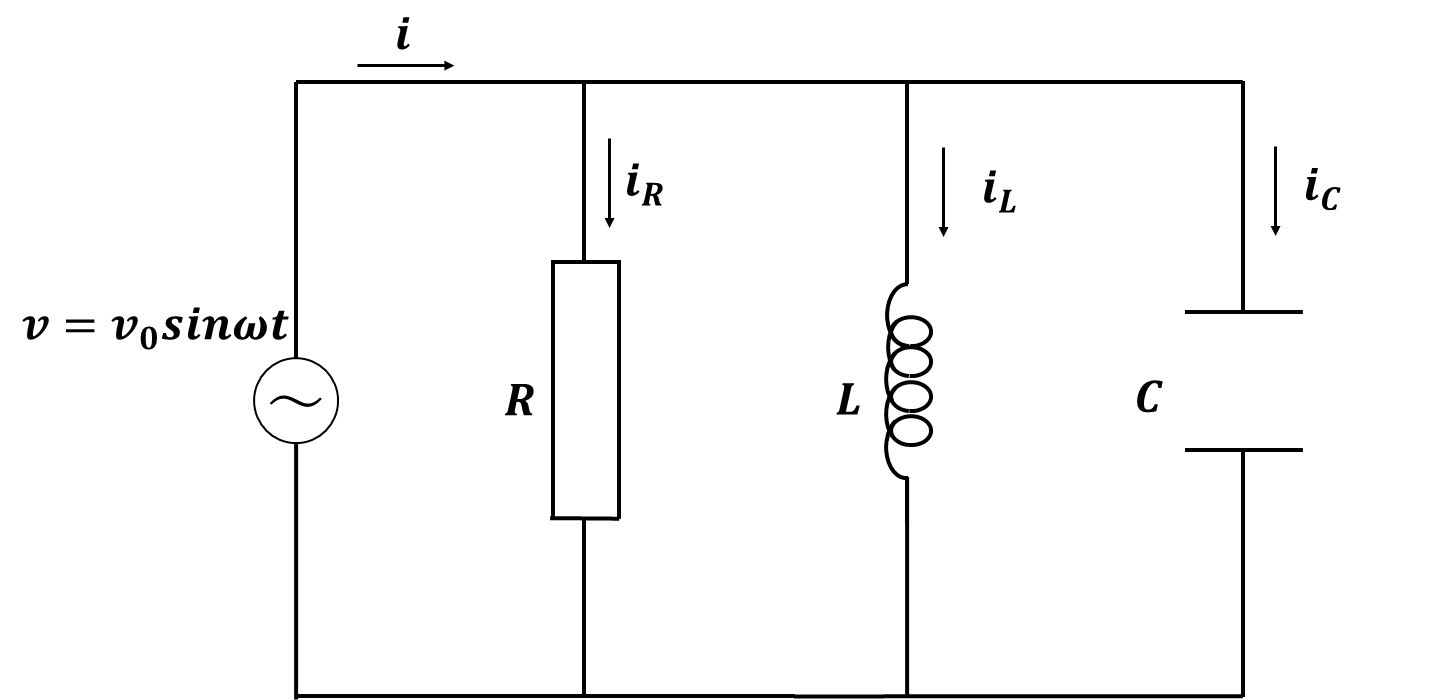
上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。

（１）\(i_R,i_C,i_L\)を求めよ。
（２）回路全体のインピーダンスZを求めよ。

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

それでは、解説していきます。

塾長

（１）の解答

例題

上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。

（１）\(i_R,i_C,i_L\)を求めよ。

交流でも直流でも、回路問題の解き方は『手順』が決まっていました。

今回は、コイルもあるので、仮定した電流とは逆向きに誘電起電力を描きましょう！

そして、前回と違うところは、今回はベクトルを使って解いていくので、このやり方をするときには、回路内の電流・電圧は、すべて最大値で仮定します！

上でたくさんのことをやっていますが、すべて描き込むと大したことはありませんよ！

悩んでる人

ん？抵抗、コイル、コンデンサーにかかる電圧の最大値も、電源電圧の最大値と同じ\(v_0\)ですか？

導線でつながっているところは、すべて等電位（高さが一緒）だから、回路を色分けすると、オレンジと水色の2色に分けられるよね？
電源電圧は、水色からオレンジに向かって、電位が\(v_0\)上がっているから、同じ色の変化をしている場所も、電位差は\(v_0\)なんだ！

塾長

交流回路では、オームの法則のようなインピーダンスの式$$X_e=\frac{v_0}{i_0}$$

がありました。これを使えば、各素子にかかる電流・電圧の最大値、インピーダンスの大きさがわかるのでした。

コイル、コンデンサーのインピーダンスは、\(\omega L,\frac{1}{\omega C}\)でしたので、それぞれの素子に対してインピーダンスの式を立てると、

$$R=\frac{v_0}{i_{R0}} \therefore i_{R0}=\frac{v_0}{R}・・・➀$$$$\omega L=\frac{v_0}{i_{L0}} \therefore i_{L0}=\frac{v_0}{\omega L}・・・➁$$$$ \frac{1}{\omega C}=\frac{v_0}{i_{C0}} \therefore i_{C0}=\omega Cv_0・・・➂$$

となります。

これで、各素子にかかる電流の最大値がわかったので、位相のずれを考えていきます。

交流の電流・電圧って、（最大値）×（基準からのタイミングのずれ）でできてるから、タイミングのずれ（位相のずれ）さえ求めてしまえば勝ちだよ！

塾長

悩んでる人

タイミングの基準ってなんですか？

今回は並列回路だから、すべての素子で電圧が変化するタイミングが同じだね！（同じ電圧がかかっているということ）

つまり、今回は電圧の位相\(\omega t\)が基準になるんだ！

塾長

電源電圧$$v=v_0sin\omega t$$を基準にすると、

・抵抗⇨位相はずれない
・コイル⇨電圧より\(\frac{\pi}{2}\)遅れる
・コンデンサー⇨電圧より\(\frac{\pi}{2}\)進む

ので、それぞれに流れる電流は、位相のずれを考慮して、

$$ \therefore　i_R= i_{R0}sin\omega t（位相はずれない）・・・➃$$$$ \therefore i_L= i_{L0}sin(\omega t-\frac{\pi}{2})（\frac{\pi}{2}遅れる）・・・⑤$$$$ \therefore i_{C}=i_{C0sin}(\omega t+\frac{\pi}{2})（\frac{\pi}{2}進む）・・・➅$$

まずは、➀を➃に代入して$$i_R=\frac{v_0sin\omega t}{R}・・・答え$$

➁を⑤に代入して、sinをcosに変換して$$i_L=-\frac{v_0}{\omega L}cos\omega t・・・答え$$

➂を➅に代入して、sinをcosに変換して$$i_C=\omega Cv_0cos\omega t・・・答え$$

となります。

このやり方は、微積を使わないので、計算が苦手な人でもできますね！

塾長

（２）の解答

例題

上の図のように、交流電源に抵抗、コイル、コンデンサーがつながれている。抵抗の大きさ、コイルの自己インダクタンス、コンデンサーの容量、および、各部分に流れる電流を図のように定めた時、次の問いに答えよ。

（２）回路全体のインピーダンスZを求めよ。

（２）は、全体のインピーダンスを求めたいので、回路全体の電流・電圧の最大値がわかればOKです。

回路全体の電圧の最大値は、電源電圧$$v=v_0sin\omega t$$の\(v_0\)なので、電流の最大値を求めてしまえば、インピーダンスを求めることができます。

回路全体の電流\(i\)は、\(i=i_R+i_L+i_C\)なので、位相のずれを考慮して作図していきます。

今回の基準位相は、並列回路なので、電圧位相が基準位相になります。

基準位相に対して、コイルは\(\frac{\pi}{2}\)遅れ、コンデンサーは\(\frac{\pi}{2}\)進むので、それを作図すると以下のようになります。

コイルとコンデンサーの矢印、どっちが長いのか気になる人もいるかもしれないけど、電流の最大値は斜辺の『長さ』で決まるから、コイルの方の矢印を長く描いても大丈夫だよ！

塾長

最大値は、斜辺の長さになるので、回路全体を流れる電流の最大値は$$v_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}$$

となります。

最後は、インピーダンスの公式を使っておしまいですね！

電圧の最大値\(v_0\)と、電流の最大値\(v_0\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}\)を

$$Z=\frac{v_0}{i_0}$$に代入して、

$$Z=\frac{v_0}{i_0}$$$$=\frac{1}{\sqrt{\left(\frac{1}{R}\right)^2+\left(\omega C-\frac{1}{\omega L}\right)^2}}・・・答え$$

となります。

インピーダンスは、抵抗みたいなものだから、直列回路と同じように、回路全体の電流と電圧を求めればいいという方針になるね！

塾長

まとめ

今回は、交流回路をベクトルを使って解いてきました。

やったことは、たった3つです。

結局、交流は『電流・電圧の最大値』と『基準位相からのずれ』さえわかってしまえば、簡単にに解けるということです。

なので、交流回路を解くときには、上の2つを意識して解くようにしましょう。