
もしかして積分を使うのですか?
そんなおびえなくていいよ(笑)今回は使うべきところだけ説明して、計算はしないから安心して!

さらに今回は、仕事の基本的な公式についても確認していきます!

それにしても、いつもと違って何か地味ですね。
今回の内容は、次の記事のための基礎作りなんだ!だから地味だけど頑張ろう!

【疑問】そもそも物理に微積は必要なのか?
結論から言うと、高校物理に微積は必要です!
こういう風に言うと、何でもかんでも微積物理をやり始める人がいます。
実は、それも間違いで、微積は『本当に使うべき場所のみで使う』のです!

一体どういうことですか?
このサイトでは、なるべく微積を使わないように努力しているけれど、微積を使った方が理解しやすい場所では微積を使って説明しているよ!

つまり、『より深く理解するのに微積を使う方がいいかどうか』という基準で微積を使っていきます!

それじゃ、今回は微積を使うのは、より理解を深めるためってことですね。
そうだね!このサイトで、微積が出てきたときには、そう思ってほしいかな!


了解しました!頑張ります!
まずは仕事の定義を確認する
それでは、まずは仕事の定義について確認していきましょう!
仕事の定義
(仕事)=(力)×(力の方向への変位)
$$W[J]=F[N]×x[m]$$
大事なのは、仕事の単位がジュール[J]であること、\(x\)が力の方向への変位ということです!

力の方向への変位??
うん!例えば、下の図を見てごらん!

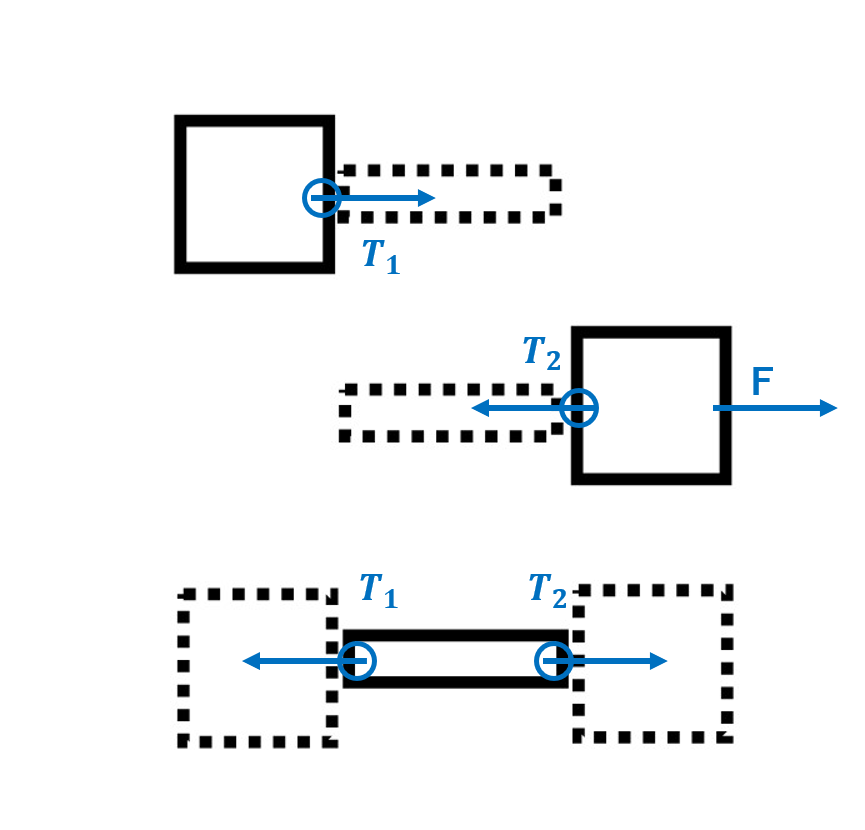
右向きに力Fが加わっていて、右にxだけ移動したら仕事はいくつかな?


\(F×x\)で答えは\(Fx\)です!
そうだね!じゃあこれは?


上向きに力Fが加わっていて、右にxだけ移動したら仕事はいくつかな?


あ!力の向きと移動した向きが違うので、仕事は0です!
その通り!だから、仕事は力の向きと、変位の向きに気を付けなくてはいけないんだ!

仕事の定義
(仕事)=(力)×(力の方向への変位)
$$W[J]=F[N]×x[m]$$
結論:力の大きさが一定でない仕事は積分せよ!

力の大きさがが一定でないときって、どんな場面ですか?
例えば、ボールペンとかに入っているばねを想像してごらん!ばねって縮むにつれて力が跳ね返す力が大きくなるよね!

ばねは、ありのまま(自然長)では力がありませんが、押し縮めたり引き延ばしたりすると、力の大きさは変化します。
つまり、ばねの力の大きさは、ばねの伸縮度によって変わるのです。
ばねのように、力の大きさが一定でない場合の仕事を求めるときには、積分を使います!

微小仕事を考える!
イメージとしては、物体がある場所で力F(x)をうけて、微小距離(少しの距離)dx移動すると考える。
これを勝手に『微小仕事』と呼ぶことにしよう。
微小距離しか移動しないから、その間では力が一定と考えられるんだ!

その微小仕事を、移動した\(x_1からx_2\)まで足し集める(積分する)と、全体の仕事Wになります!

なるほど!微小距離の移動では、力が一定だとみなして、微小仕事を足せばいいのですね!
微小仕事は、力が一定の仕事ですから、公式通り(力)×(力の方向への変位)で求められるので、
$$F(x)×dx$$
と表せます。
これを、仕事を考えたい区間で足し集める(積分する)

そうすると、こうなる式になります!

最初は難しそうと思ったけど、意外と理解できました!
ポイント
力が一定でない仕事は、微小仕事を考えて積分する!
まとめ:物理の問題では微積を使う場所を見極めるべし!
今回は、物理で微積を使うべきかどうかについてと、物理,積分,使うべきかどうか,高校物理,仕事,公式,について紹介してきました!
物理において微積は、非常に便利な計算方法ですが、微積を使うことで理解が浅くなったり、苦手になってしまっては元も子もありません。
物理で、微積を使う時は、『本当に微積を使わなくてはいけないのか』ということを考えながら、使うようにしましょうね!


