難しい問題ってどんな問題ですか?
今回は、最初に問題を出してしまおうか!

例題

水平面となす角θのあらい斜面がある。ばね定数kの軽いばねの一端を斜面上端に固定し、質量mの物体を結びつける。物体を自然長の位置から静かに放す。斜面を滑り降り、斜面に沿って長さ\(l\)だけ離れた位置を初めて下向きに通過するときの物体の速さを求めよ。重力加速度の大きさを\(g\)、物体と斜面の間の動摩擦係数を\(\mu'\)とし、物体の大きさは無視しても良いものとする。また、斜面は床に固定してあり、動かないものとする。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
よくやってしまいがちな解き方
さて!君ならどうやって解く??


斜面を滑り降りるので、\(v^2-{v_0}^2=2ax\)の公式が使えそうです!\(xをl\)として解けば\(v\)がわかります!
まんまと引っかかったね(笑)その公式が使えるのは、等加速度運動の時だけだよ!


確かに、\(v^2-{v_0}^2=2ax\)の公式を使えば、距離\(l\)が簡単に出てしまいそうですが、今回はこの公式が使えません!
なぜか。それは、物体がばねと繋がっているからなんです。
ばねの強さは、ばね自身の伸縮度によって力の大きさが変化するので、物体の加速度は場所によって変化してしまうのです。

なるほど!つまり、等加速度運動じゃないから、\(v^2-{v_0}^2=2ax\)の公式が使えないのですね!
ポイント
ばねのついた物体は、途中で速度が変化するので、等加速度運動の公式が使えない!
こんな時は、エネルギー保存則を使って解いていきます!
問題の解説
例題

水平面となす角θのあらい斜面がある。ばね定数kの軽いばねの一端を斜面上端に固定し、質量mの物体を結びつける。物体を自然長の位置から静かに放す。斜面を滑り降り、斜面に沿って長さ\(l\)だけ離れた位置を初めて下向きに通過するときの物体の速さを求めよ。重力加速度の大きさを\(g\)、物体と斜面の間の動摩擦係数を\(\mu'\)とし、物体の大きさは無視しても良いものとする。また、斜面は床に固定してあり、動かないものとする。
さて、それでは解いていきましょう!
1.力を描き込む
力の描き方
1.着目物体の数だけ図を描く!
2.場から受ける力(重力や静電気力)を描き込む!
3.他物体との接触点に印をつけ、そこを根本として、物体が受ける接触力のみを描く!
力学の問題の初めは、必ずこれでしたよね!
力の描き方について、しっかり学びたい人は、【力学の間違いの8割はここ!予備校では教えてくれない力の書き方を例題とともに徹底解説!】から。
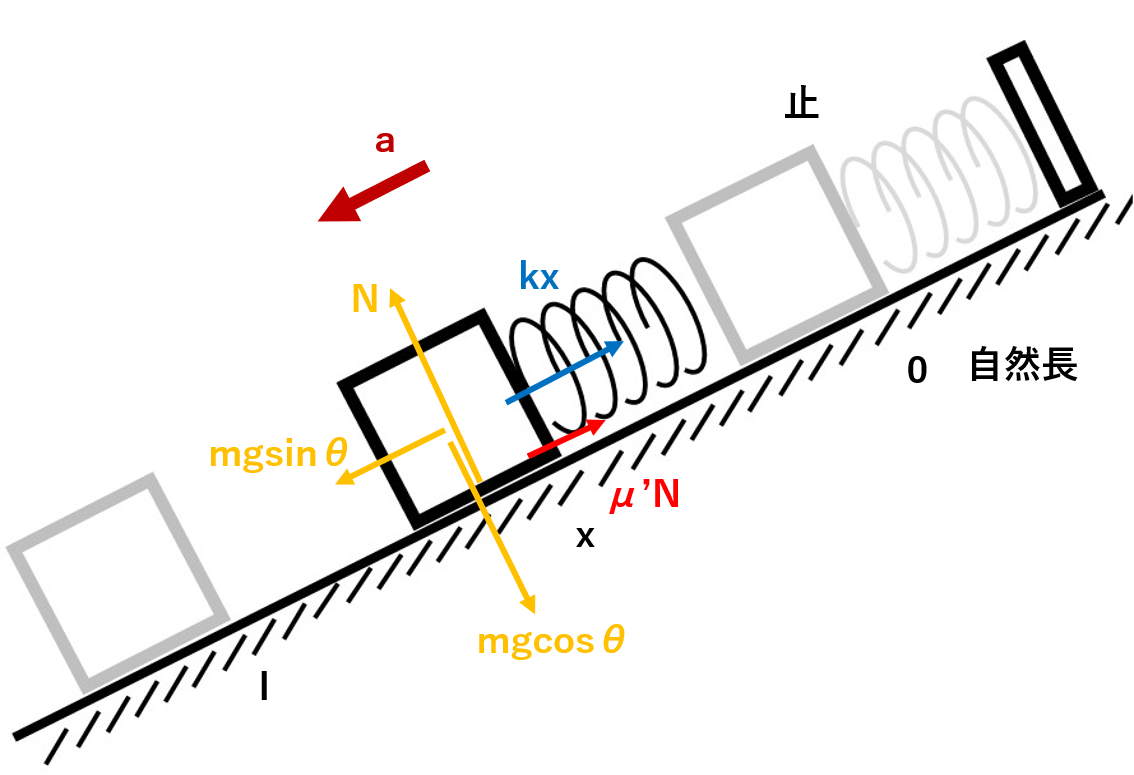
さて、上のやり方に沿って力を描き込むと、下のようになります。
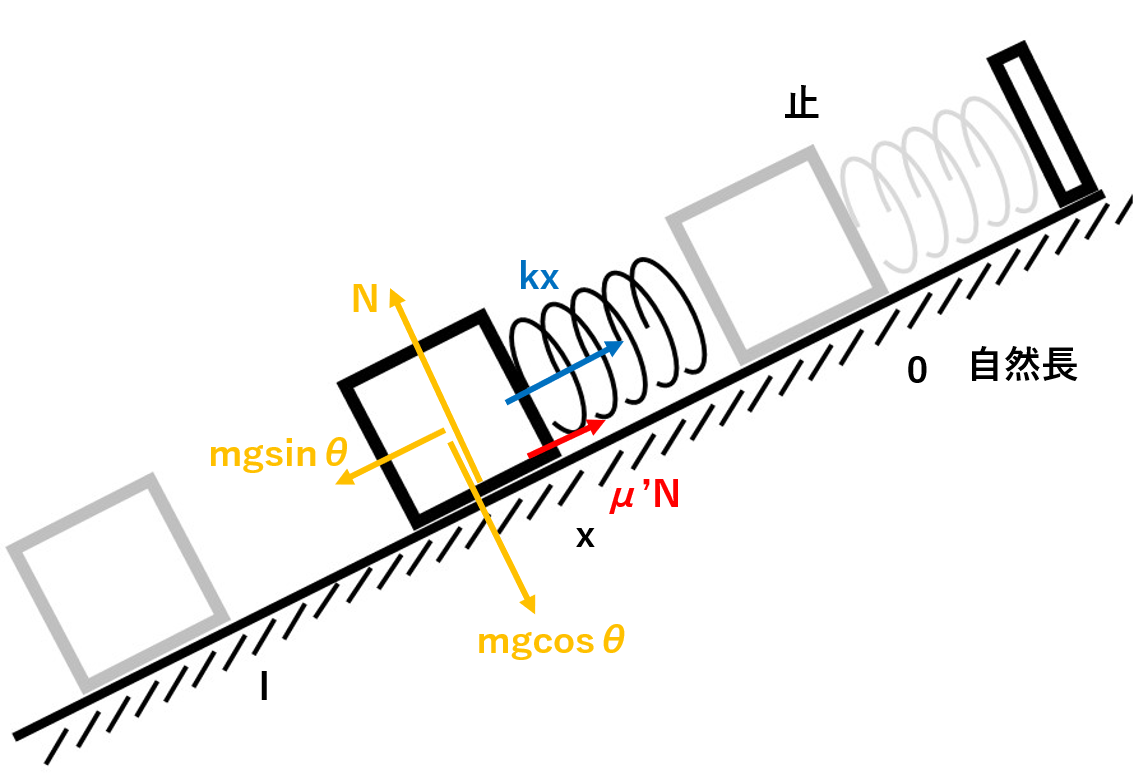
2.運動方程式を立てる!
ポイント
運動方程式を立てるときには、加速度方向を正方向として軸を決め、軸と同じ方向の力はプラス、逆ならマイナスとして考えよ!!
まずは、加速度方向に軸を立てますが、今回は左下向きに動くので、左下方向を正方向としましょう!

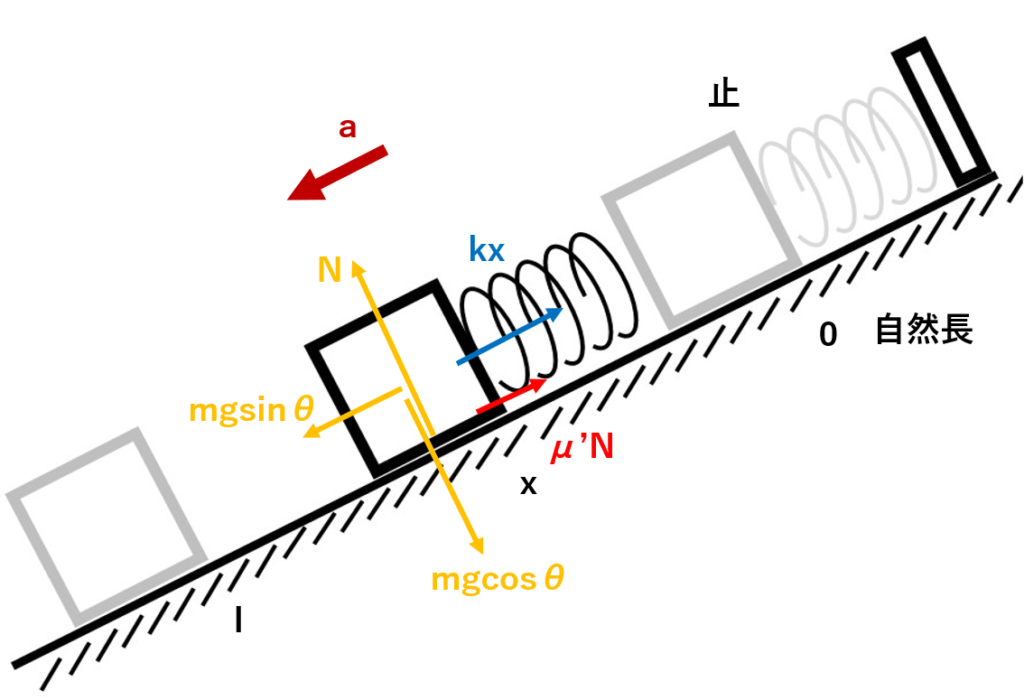
図を見て、軸と同じ方向の力はプラス、逆ならマイナスとして考えればいいので、運動方程式は
$$ma=mgsin\theta-\mu'mgcos\theta-kx$$
※\(N=mgcos\theta\)より、\(\mu'N=\mu'mgcos\theta\)
となります!
導出方法を知っていれば頭を使わず一発で式が立つ!
ここから下は、参考書にも書いていない、エネルギー保存の式の立て方です!
紹介する前に、まだ【エネルギーと仕事の関係をあなたは導出できますか?物理の問題を解くうえでどういう時に使うべきかについて徹底解説!】の記事を読んでいない人は、先にこの記事をチェックしておいてください。
さて、エネルギーと仕事の関係の式は、運動方程式から導出できることを前回勉強しました。
$$ma=mgsin\theta-\mu'mgcos\theta-kx$$
つまり、この問題でも、上の運動方程式をエネルギーの式に変換することができるのです!

どういうことですか?
エネルギーと仕事の関係の式は、運動方程式が下のような形に変化したよね!

エネルギーと仕事の関係の式
$$ma=F$$
⇩
$$\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2=Fx$$
『運動エネルギーの変化量』=『仕事』
同じように、運動方程式の\(ma\)側を運動エネルギーの変化量、運動方程式の\(F\)側を仕事に、見比べながら書き換えると、
運動方程式をエネルギー保存の式に
$$ma=mgsin\theta-\mu'mgcos\theta-kx$$
⇩
$$\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2=mgsin\theta×l-\mu'mgcos\theta×l-\int^l_0 kxdx$$
『運動エネルギーの変化量』=『仕事』

なるほど!右辺を仕事にしたければ、一定の力なら単純に距離をかけて、変化する力なら距離で積分するのですね!
その通り!運動方程式からエネルギーと仕事の関係が導けることを知っていれば、こうやってエネルギー保存の式を立てられるんだ!

よく、エネルギー保存の式を立ててごらん、というと、符号を間違えたり、摩擦のする仕事を右辺と左辺、逆に書いてしまう人が多いけど、この立て方なら、上のような心配はありません!
ポイント
複雑なエネルギー保存の式は、運動方程式を見ながら式を立てよ!
$$\frac{1}{2}mv^2-\frac{1}{2}m{v_0}^2=mgsin\theta×l-\mu'mgcos\theta×l-\int^l_0 kxdx$$
この式の\(v_0\)は、初速度なので、今回の問題の場合は、静かに放したので\(0\)。
さらに、右辺の積分をして、
$$\frac{1}{2}mv^2-0=mgsin\theta×l-\mu'mgcos\theta×l-\frac{1}{2}kl^2$$
よって、\(v\)を求めると、
$$v=\sqrt{2glsin\theta-2\mu'glcos\theta-\frac{kl^2}{m}}$$
となります。
まとめ
今回は、参考書に載っていないエネルギー保存の式の立て方について紹介しました!
運動方程式からエネルギーと仕事の関係が導けることを知っていれば、同じようにエネルギー保存の式を立てられることがわかっていただけたのではないでしょうか。
物理において、導出を学ぶことがいかに大切かということもわかってもらえたと思うので、公式の導出は積極的にやっていきましょう!
それが、物理の成績を爆上げするのに必要な勉強法の一つです。
合わせて読みたい!