
・電磁気の回路問題が苦手
・RL回路の解き方がわかりません
・回路の中のコイルの扱い方がわかりません
この記事を読めば、上の悩みは確実に解消されます!
参考書には、あたかも解き方がたくさんあるような書き方をしていますが、実は、回路問題の解き方は、たった1つしかありません。
その方法を知っている人は、このページを閉じてもらっても構いませんが、知らない人はぜひこのページを読んでみてください。
✔この記事の内容
・回路の中にあるコイルの扱い方
・RL回路の解き方
・コイルを流れる電流の時間変化のグラフ
✔この記事の信頼性
苦手だった物理を、浪人時に偏差値65以上センター試験満点近くまで伸ばした、参考書には書かれていない、考え方や勉強法について、必要なエッセンスを『ぎゅっと』凝縮してまとめています。
回路の中にコイルがあるときの解き方
そもそもコイルは、人間と同じで『変化を嫌う』という性質があります。
例えば、コイルにいきなり電流が流れようとすると、流さないようにしたり、逆にコイルに流れる電流が減りそうになったら、自分で電流を増やしたりするのです。

なんかコイルに共感できます、、
ですが、コイルはある程度環境に慣れてくると、普通の導線に戻ってしまうという性質もあります。
つまり、『コイルは環境の変化を妨げようとするけれど、環境に慣れてくると導線になる』ということです。
上の内容を踏まえると、コイルは回路の中では、下のような振る舞いをします!

ココがポイント
➁十分時間後:\(\frac{dI}{dt}=0\)⇨電流変化は0
さらに、自己誘導・相互誘導のところで、電流が流れる方向を正方向とした時、コイルが作る誘電起電力の大きさは、
$$V=-L\frac{dI}{dt}$$
となることを勉強しました!
※知らない人は、【自己誘導・相互誘導は漫才コンビ?!インダクタンスの導出をわかりやすく解説】をチェック!
さて、ここで大切なのは、『誘電起電力は、電流の正方向と逆向きに発生する』ということです!
それなら最初から、『電流と逆向きを誘電起電力の正方向』にしてしまえばいいのです!

そうすると、コイルが作る誘電起電力は、電流の向きと逆向きを正方向とした時、
$$V=L\frac{dI}{dt}$$
と考えることができてしまうのです。

なので、回路の中にコイルがあったときは、『仮定した電流とは逆方向に、誘電起電力\(L\frac{dI}{dt}\)』を取ってあげればよいのです。
RL回路問題の解き方
例題
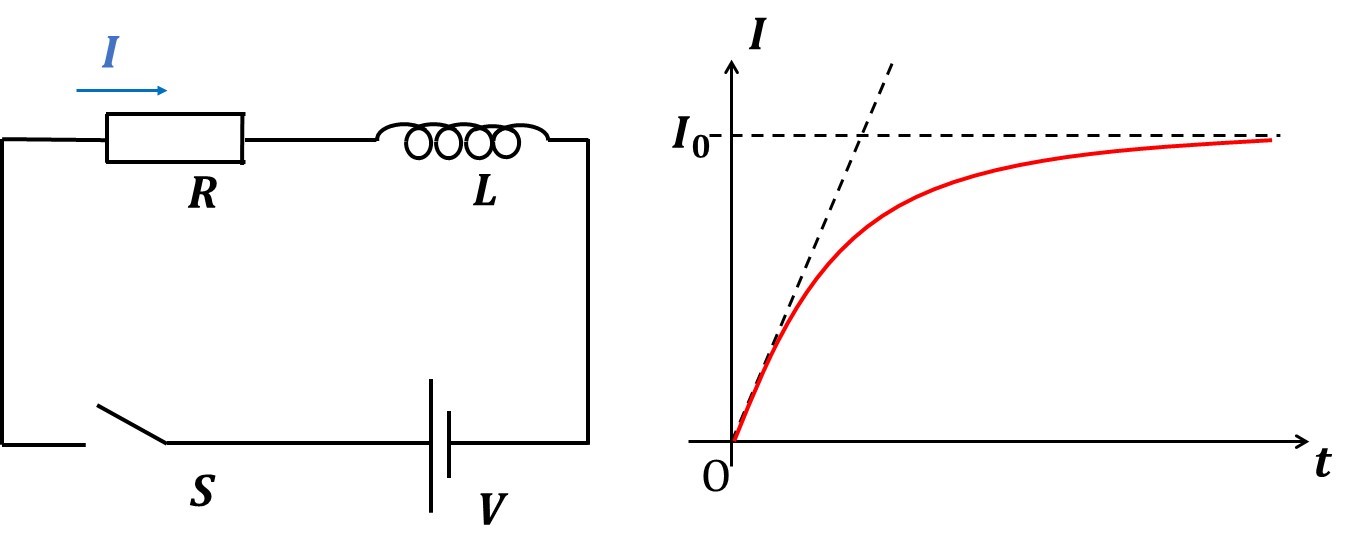
上のような回路で、スイッチSを閉じた時に回路に流れる電流の時間変化を測定したところ、右にあるグラフのような形で変化した。コイルの電気抵抗や電池の内部抵抗はないものとする。
(1)十分時間がたった時に回路に流れる電流\(I_0\)を求めよ。
(2)\(t=0\)のときのグラフの傾きを求めよ。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
それでは、解いていこう!

(1)の解答
例題

上のような回路で、スイッチSを閉じた時に回路に流れる電流の時間変化を測定したところ、右にあるグラフのような形で変化した。コイルの電気抵抗や電池の内部抵抗はないものとする。
(1)十分時間がたった時に回路に流れる電流\(I_0\)を求めよ。
さて、回路問題では、どんな問題でも、以下のような解き方で解くことができます。
回路問題の解き方
➁オームの法則を使って抵抗にある未知数を求める
➂回路方程式を立てて、電荷や電流を求める
※回路方程式とは、キルヒホッフの法則(電流保存、電位1周で電位差0)や電荷保存の式のこと
そして、必ず電位が高い方に矢印の先端を描きましょう!

上の内容はめちゃくちゃ大事なので、ノートにメモっておこう!!
さて、➀➁を描いてしまうと、下のようになります。
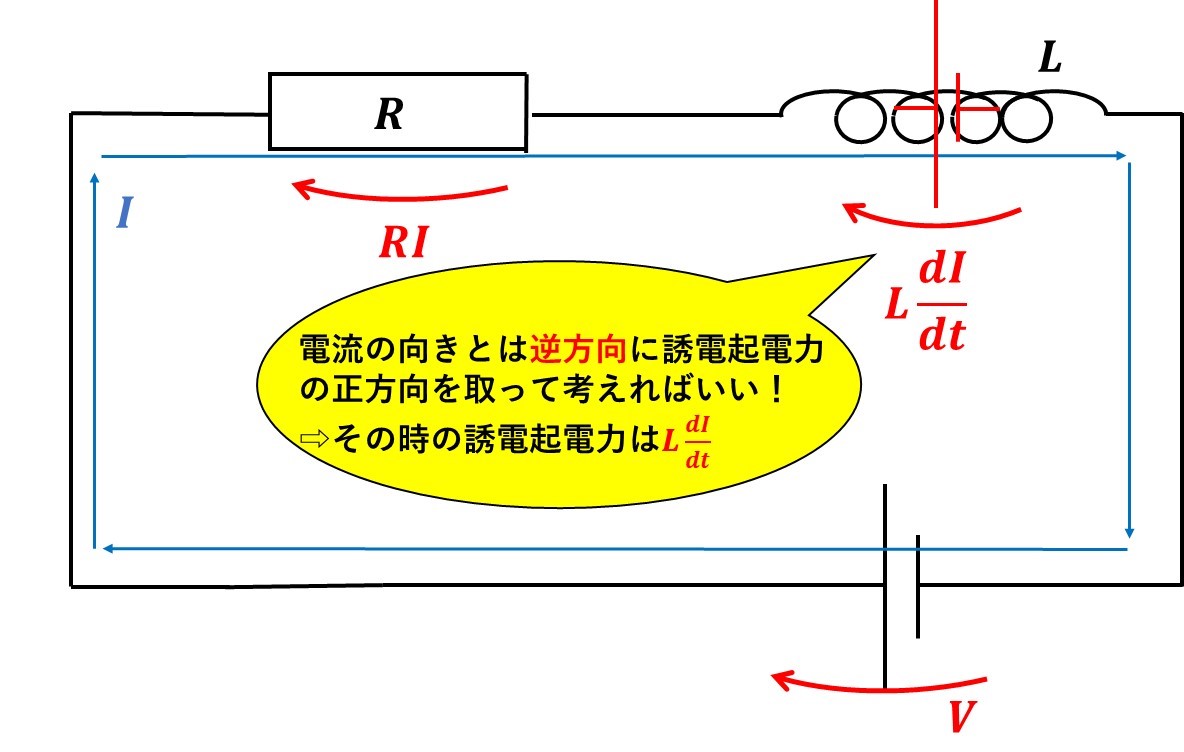
ここまで描けたら、➂の回路方程式を立てていきます。
・回路内に枝分かれがない⇨電流保存は使わない
・コンデンサーがない⇨電荷保存は使わない
ので、回路方程式は、電位差が回路一周して0の、キルヒホッフの第二法則を使うしかありません。

矢印の先端が高電位なので、根元から先端に向かってなぞれば上昇、逆なら下降です。
電池のところから時計回りになぞると、電位差は
$$+V-RI-L\frac{dI}{dt}=0$$$$\therefore L\frac{dI}{dt}=V-RI・・・➀$$
となります。

微分の形になっている\( L\frac{dI}{dt}\)のところが、何となく嫌です
そんな時は、言葉で置き換えるのをおすすめするよ!
例えば、\(\frac{dI}{dt}\)は(電流)の(時間)変化みたいに、(分子)の(分母)変化と訳すことができるんだ!

コイルの性質より、十分時間後は環境にもなれてくるので、誘電起電力を作らなくなるので、電流の時間変化は0になります。
つまり、➀の式の中にある\(\frac{dI}{dt}\)は0になるので、
$$ L\frac{dI}{dt}=V-RI・・・➀$$$$ L・0=V-RI$$$$\therefore I_0=\frac{V}{R}・・・答え$$
となります。
【大切】コイルのグラフは終端速度型になる
空気抵抗がある空間に、物体を放して自由落下させると、運動方程式は
$$m\dot{v}=mg-kv$$
となります。
ドットは、微分という意味で、加速度は『\(v\)ドット』の形で書きました!
さらに、v-tグラフの概形を描くと、以下のようになります。

※さらに、詳しく知りたい人は【終端速度って何?空気抵抗がある物体の運動について例題とともに解説!】をご覧ください。
ここで(1)で出てきた式をみてみよう。
$$ L\frac{dI}{dt}=V-RI・・・➀$$
$$m\dot{v}=m\frac{dv}{dt}=mg-kv$$

あ!終端速度の運動方程式と形が似ています!
終端速度の方は、\(\dot{v}\)と\(v\)の一次関数になっていて、今回は\(\dot{I}\)と\(I\)の一次関数になっているから、まったく同じ形だね!

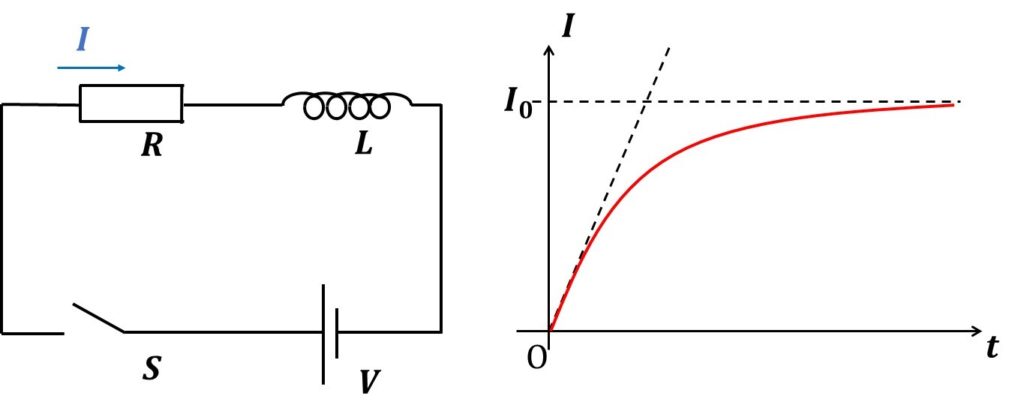
終端速度のグラフから、コイルを流れる電流の時間変化のグラフを描くことができることも、覚えておきましょう!
(2)の解答
例題

上のような回路で、スイッチSを閉じた時に回路に流れる電流の時間変化を測定したところ、右にあるグラフのような形で変化した。コイルの電気抵抗や電池の内部抵抗はないものとする。
(2)\(t=0\)のときのグラフの傾きを求めよ。
グラフの傾きは、縦軸が『電流』で、横軸が『時間』なので、『電流の時間変化』つまり$$\frac{dI}{dt}$$がグラフの傾きになります。
\(t=0\)のとき、グラフをみると電流が0なので、➀式から
$$ L\frac{dI}{dt}=V-RI・・・➀$$$$ L\frac{dI}{dt}=V-R・0$$$$\therefore \frac{dI}{dt}=\frac{V}{L}・・・答え$$
となります。
まとめ:コイルの扱い方を覚えてRL回路の問題を攻略しよう!
今回は、RL回路を例に、コイルが入った回路問題の解き方について話してきました。
ポイントは、以下のところになります!

参考書には、かなりごちゃごちゃ書かれている部分かと思いますが、上のような解き方で解けば、どんな問題でも必ず解けます。
自分の持っている問題集でも、コイルの問題にチャレンジしてみてくださいね。

