
相対速度って、求めるときにいつも間違ってしまうんですよね。
こんな悩みを持っている人も多いのではないでしょうか。
そこで今回は、相対速度の求め方について紹介していきます!
この記事を読めば、後々説明する『はね返り係数』の話も理解できますので、しっかり勉強していきましょう。
目次
【結論】相対速度は"相手-自分"で考えればOK!
相対速度とは、観測者からみた相手の速度のことを言います!
そして、相対速度は、【相手の速度ー自分の速度】で求めることができるのです。
相対速度
相対速度は、【相手の速度ー自分の速度】で求める!

うーん、イマイチまだわからないです。
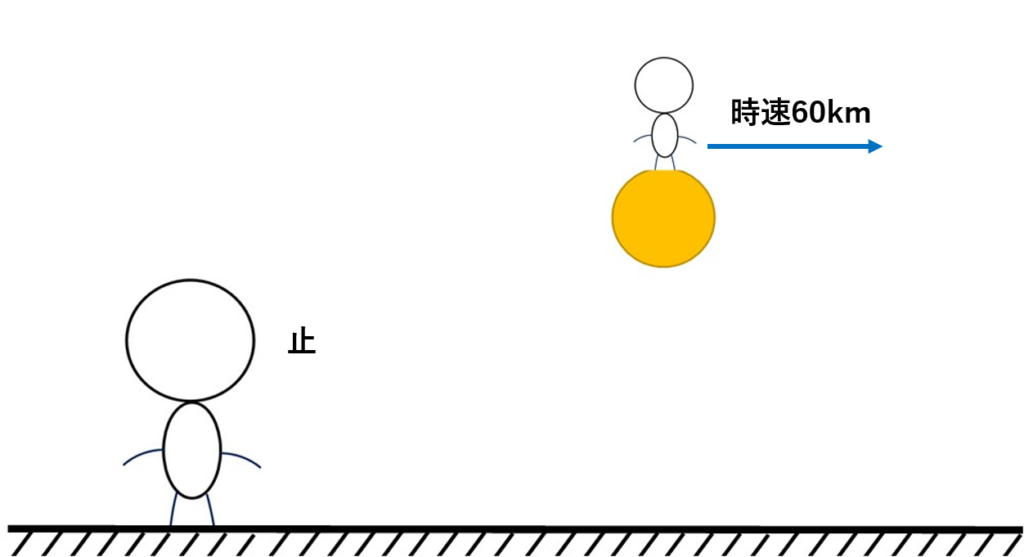
例えば、上のように2人がいて、一人は地面に、もう一人は時速60kmのボールの上にいるとしようか。この時ボールの相対速度について求めてみよう!

相対速度の考え方①:止まっている人から見る

まずは、観測者が地面にいるときを考えましょう!
相対速度は、『相手の速度ー自分の速度』で求められるから、今回は、(ボールの速度)-(止まっている人の速度)となる。
つまり、\(60km-0km=60km\)となります!
相対速度の考え方②:ボールの上にいる人から見る

続いて、観測者がボールの上にいるときの、相対速度を考えます!
同じように相対速度は、『相手の速度ー自分の速度』で求められるから、今回は、(ボールの速度)-(ボールの上の人の速度)となる。
つまり、\(60km-60km=0km\)となります。
動いている物体の上に乗ってみれば、確かに相対速度は0kmだよね!

相対速度
相対速度は、【相手の速度ー自分の速度】で求める!
一直線上でないなら相対速度はベクトルで考える!
例えば、下の例題を見てみよう!

例題
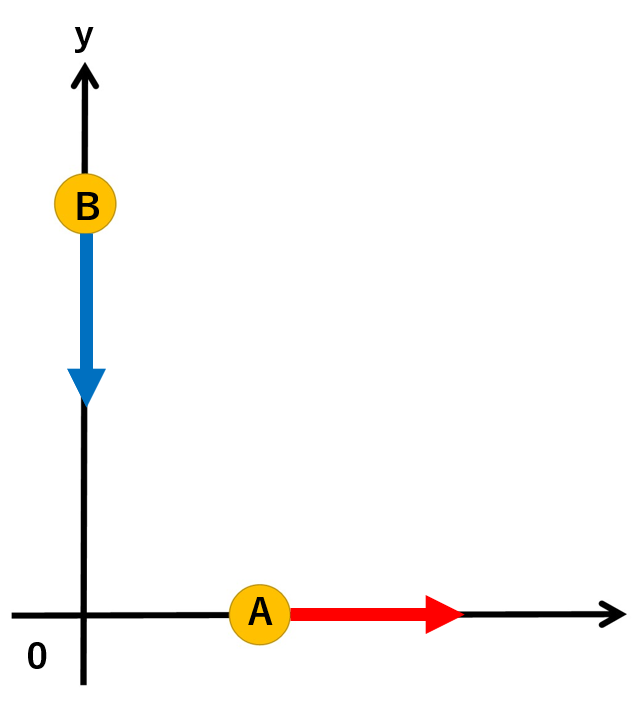
x軸上とy軸上に、矢印の向きに10m/sの速さで進む2つの物体がある。Bから見たAの相対速度を求めよ。(明快解法講座より引用)
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!

これも、『相手の速度ー自分の速度』で考えればいいのですよね?
そうだね!けれど、どちらの物体も動く方向が一直線上にないよね。そんな時はベクトルで考えるんだ!

ポイント
物体が、同一直線上で動かないときは、ベクトルで考える!
⇨ベクトルの合力が相対速度になる!
【解法】相対速度をベクトルで解く

それでは解いていきましょう!
今回は、BからAを見た時の相対速度なので、Bの上に観測者(自分)が乗ります!
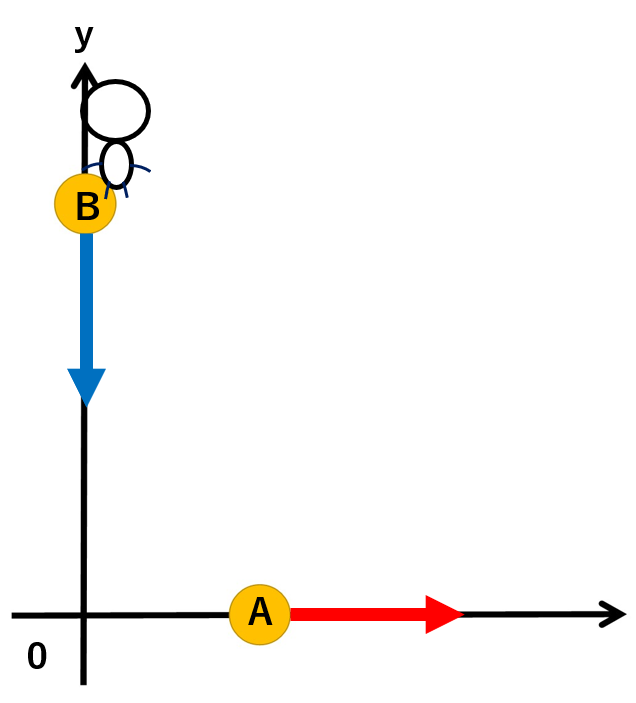
相対速度は、相手の速度ー自分の速度なので、今回は(Aの速度)-(Bの速度)となります!
さらに、今回の場合は、運動が一直線上ではないので、ベクトルで考えると、
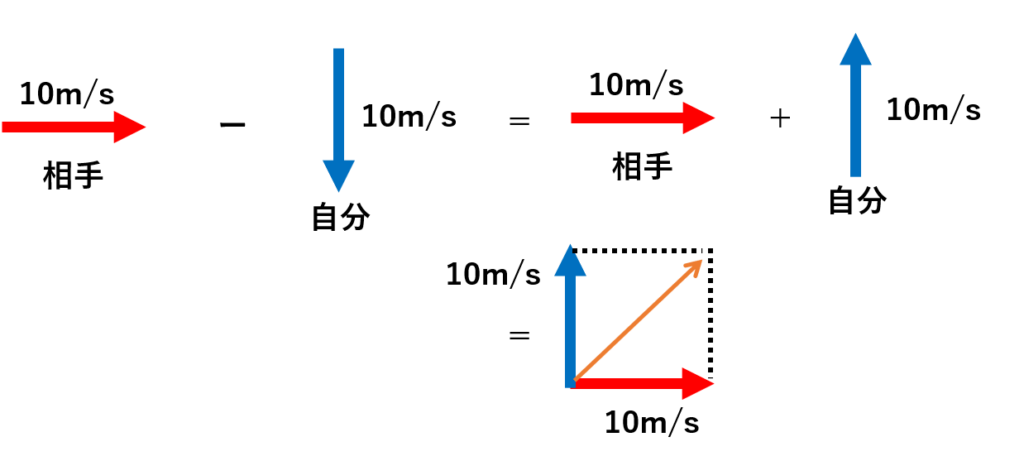

なるほど!『相手の速度ー自分の速度』を同じように、ベクトルで考えるのですね!
その通り!『マイナス自分の速度』のところはプラスに直して、矢印の向きを逆にすればOK!

ベクトルで考えた時の相対速度は、ベクトルの合力になるので、オレンジの矢印の大きさは、\(10\sqrt{2}\)となります!
まとめ:相対速度の公式は「相手-自分」で考える!
今回は、相対速度について説明しました!
相対速度についてまとめると、以下のようになります!
相対速度のまとめ
1.相対速度は、【相手の速度ー自分の速度】で求める!
2.物体が、同一直線上で動かないときは、ベクトルで考える!
⇨ベクトルの合力が相対速度になる!
相対速度の求め方について理解していれば、はね返り係数の理解も簡単なので、しっかり覚えておいてください!


