
・熱力学の問題が解けない
・どの式を立てたらいいかわからない
・問題の解き方がわからない
今回は、そんな悩みを解決していきます。
熱力学の範囲では、さまざまな式が登場するので、問題を解くときにどの式を使っていいかわからなくなりますよね。
私も、以前は同じように苦しんでいたのですが、解法がたった4つに絞られることがわかってから、熱力学の問題で間違えたり、まったく解けないといったことはなくなりました。
皆さんもこの記事を読めば、私と同じような思考を持つことができるので、しっかりと勉強していきましょう。
✔この記事の内容
・熱力学の式の立て方は4つのみ!
・特殊な気体の状態方程式の立て方
・問題を解くうえで、初めにやること
✔この記事の信頼性
浪人時に苦手だった物理を、記述模試偏差値65以上、センター試験満点近くまで伸ばした『考え方』や『解き方』について、大切なエッセンスを『ぎゅっと』凝縮してまとめています。
目次
【高校物理】熱力学の解法パターンはたった4つ!
力学の問題の解き方のフローシートでもやりましたが、熱力学の解き方もやるべきことが決まっています!
※力学のフローシートはこちらから無料配布しています。
熱力学の解き方
➁運動方程式(つり合いの式)
➂エネルギー収支(熱力学第一法則)
➃ポアソンの式(断熱かつ熱平衡のとき)
熱力学の問題は、基本的に上の4つのみで解くことができます!
では、実際に問題を解いていきましょう。
例題:ばねつきピストン
例題

断面積がSのシリンダーが鉛直に立ててある。ピストンとシリンダーの底とは自然長がhのばねでつながれている。また、シリンダー交換の底から測って高さhのところに、ストッパーsがある。このシリンダー内にある量の単原子分子の理想気体を、大気圧\(p_0\)と同じ圧力になるまで封入した。この時、ピストンはストッパーの位置にあり、絶対温度は\(T_0\)であった(状態1)。次に、シリンダー内をゆっくり加熱したところ、温度が\(2T_0\)になったところで、ピストンが上昇し始めた(状態2)。さらに加熱したところ、温度が\(6T_0\)となったとき、ピストンは\(\frac{h}{2}\)だけ上昇した(状態3)。
(1)ピストンの質量を求めよ、ただし、重力加速度の大きさを\(g\)とする。
(2)状態1から状態3まで気体のした仕事を、\(p_0,S,h\)で表せ。
(3)状態1から状態3までに加えられた熱量を、\(p_0,S,h\)で表せ。
(明快解法講座を改題)
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
熱力学の問題を解く前にやること!
まずは、各状態におけるP,V,n,Tを図示しましょう。
この時、未知数(自分で置いた文字)は、〇で囲んでおきましょう!


上のように、各状態における力も描き込んでしまいましょう!
つぎに、どの式を立てるか考えます。
熱力学の解き方
➁運動方程式(つり合いの式)
➂エネルギー収支(熱力学第一法則)
➃ポアソンの式(断熱かつ熱平衡のとき)
熱力学は、以上4つの式のみを考えればいいので、それぞれについて考えていきましょう。
今回の変化は、断熱変化ではないので、➃のポアソンの式は、使うことができません。
なので、まずは➀➁の状態方程式とつり合いの式を立てていきます。
その①:状態方程式
$$nR=\frac{p_0Sh}{T_0}=\frac{p_1Sh}{2T_0}=\frac{p_2S\frac{3}{2}h}{6T_0}$$
(定数)=(状態1)=(状態2)=(状態3)
その②:つり合いの式
$$(状態2)p_1S=p_0S+Mg$$$$(状態3)p_2S=p_0S+Mg+k\frac{h}{2}$$

気体の状態方程式が見たことない形で書かれているのですが、、
気体の状態方程式は、各状態をつなぐ式で、今回はずっとモル数が変化しないから、すべての式をつなぐことができるんだ!

気体の状態方程式をつないで書くことで、計算しやすい部分同士で計算できるようになります!
ココがポイント
(1)の解答:熱力学の問題
$$nR=\frac{p_0Sh}{T_0}=\frac{p_1Sh}{2T_0}=\frac{p_2S\frac{3}{2}h}{6T_0}$$
(定数)=(状態1)=(状態2)=(状態3)
ピストンの質量を求めていきます。状態1と状態2の式から
$$p_1=2p_0・・・➀$$
となります。
つり合いの式、
$$(状態2)p_1S=p_0S+Mg$$
に➀を代入して、
$$2p_0S=p_0S+Mg$$$$\therefore M=\frac{p_0S}{g}・・・答え$$
となります。
(2)の解答:熱力学の問題
状態1から状態3までの間に、気体がした仕事は、1から2が定積変化で仕事をしないことから、2から3までの仕事と等しくなります。
注意することは、状態2から3の間で、気体の圧力が変化することだよ!

ココに注意

気体の状態方程式の状態1、3から、\(p_2=4p_0\)であることがわかります!
オレンジの部分が気体がした仕事なので、台形の面積を求めると、
$$(2p_0+4p_0)×\frac{1}{2}Sh×\frac{1}{2}$$$$=\frac{3}{2}p_0Sh・・・答え$$
となります。
(3)の解答:熱力学の問題
状態1から状態3までの間に、加えられた熱量は、熱力学第一法則に基づいて考えることができますね!
熱力学第一法則
内部エネルギー変化は、今回単原子分子なので、$$\Delta U=\frac{3}{2}nR\Delta T$$と考えることができます。
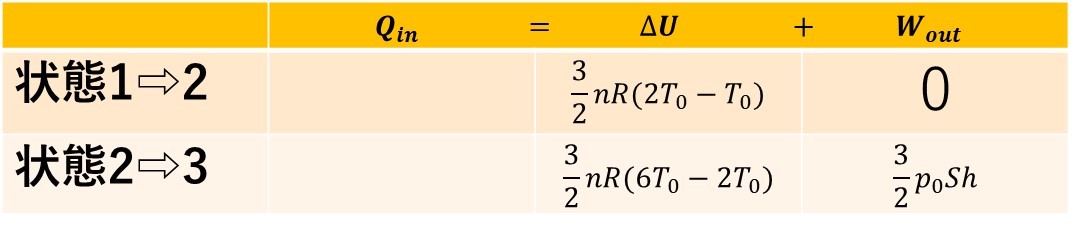
各状態の温度変化に注意して、内部エネルギー変化と、仕事について書くと、上のようになります。
答えに、n,Rは使ってはいけないので、気体の状態方程式$$nR=\frac{p_0Sh}{T_0}$$を使って書き替えると、以下のようになります。

この表から、\(Q_{in}\)を求めると、
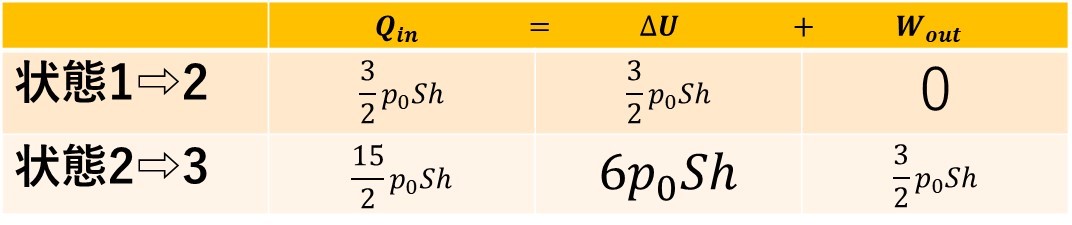
上のようになります。
よって、吸熱の合計は、
$\frac{3}{2}p_0Sh+\frac{15}{2}p_0Sh=9p_0Sh・・・答え$$$
となります。
まとめ:熱力学は解き方が決まっているので簡単!

今回は、熱力学の解法について話してきました。
大切なのは、熱力学で立てるべき式は4つしかないということです!
熱力学の解き方
➁運動方程式(つり合いの式)
➂エネルギー収支(熱力学第一法則)
➃ポアソンの式(断熱かつ熱平衡のとき)
上に加えて、
・気体の状態方程式はつなげて書く!
・それぞれの状態に合わせて図を描く!
ことも大切なので、上のことを意識しながら問題を解いてみましょう!

