
先生!ガウスの法則の4πkQ本って何ですか?
4πkQ本は、『任意の閉曲面内にある、電荷Qから湧き出す電気力線の本数』だよ!

ガウスの法則で、『4πkQ本って何??』と思った経験ありませんか?
そこで今回は、『どうして4πkQ本になるのか』について例題を絡めて詳しく説明していきます!
⇩前回の電気力線の記事をまだ見ていない人は、先にこちらを見るのをお勧めします。
合わせて読みたい!
電気力線と電場の関係

前回の内容で、電気力線は、『電場を視覚化したもので、\(+1\)クーロンが、電場から\(F=qE\)の力を受けて移動した道筋』でしたね!
しかも、電気力線には、以下のような特徴がありました。
電気力線の特徴!
1.途中で枝分かれしない
2.電気力線の向き=電場の向き
3.電気力線は、+からでて-に入る

電気力線から、電場の向きがわかるんでしたね!
そうだね!しかも電場の強さも電気力線からわかったよね。


同じ面積で囲ってあげた時に、電気力線の本数が多いと、電場も強いんですよね!

その通り!ある部分ではなく、\(1m^2\)で囲った部分の電気力線の本数を、ガウスの法則というよ!

電気力線とガウスの法則は、密接につながっています!
では、ガウスの法則とはどのような法則なのでしょうか。
電場のガウスの法則
電場のガウスの法則の定義は、以下の2つになります!
定義は物理において、非常に重要なのでしっかり覚えておこう!

ガウスの法則
・\(1m^2\)あたりの電気力線の本数=その点の電場の強さ
・任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例し、
$$4{\pi}k_0Q本=\frac{Q}{\varepsilon_0}本$$
\(k_0=\frac{1}{4\pi\varepsilon_0}\)で、\({\varepsilon_0}\)のことを真空の誘電率というよ!

上の法則で、覚えておくべきことは、『電荷Q』を『真空の誘電率\({\varepsilon_0}\)』で割ると、電気力線の本数になるということです!
それでは、これを導出していきましょう!

ガウスの法則の導出
以下の例題を使って、ガウスの法則を導出していきます!
大切な導出ですので、必ず自分で手を動かしてやりましょう。
例題
クーロンの法則の比例定数を\(k_0\)とする。\(+Qの正電荷からrだけ離れた点の\)電場の強さ\(E=k_0\frac{Q}{r^2}\)を用いて、正電荷からわきだす電気力線の本数を求めよ。
※答えを見る前に、まずは自分で考えてみましょう!

なんか難しそうなんですけど、、、
大丈夫!まずは電場と電気力線の関係から復習しよう!

そもそも電場と電気力線の間には、\(1m^2\)あたりの電気力線の本数=その点の電場の強さという関係がありました。

点電荷は本来、2次元ではなく3次元です!
上の画像のように、電荷の中心から距離rだけ離れた場所の電場の強さは\(E=k_0\frac{Q}{r^2}\)ですから、黄色の\(1m^2\)で切り取ると、\(1m^2\)あたりの電気力線の本数になります!
$$E×1m^2本=k_0\frac{Q}{r^2}×1m^2本=(電気力線の本数)$$
となります。
これは、あくまで\(1m^2\)あたりの電気力線ですから、正電荷から湧き出す電気力線の本数が知りたければ、正電荷をすべて囲ってあげる必要があります。
では、正電荷を距離rの部分で囲うと、面積はいくつかな?


正電荷は球なので、半径rの球の表面積\(4{\pi}r^2\)です!
\(1m^2\)あたりの電気力線の本数は、
$$E×1m^2本$$
でしたので、\(4{\pi}r^2\)あたりの電気力線の本数(=正電荷から湧き出す電気力線の総本数)は、
$$E×4{\pi}r^2本=k_0\frac{Q}{r^2}×4{\pi}r^2本$$
$$=4{\pi}k_0Q本$$
となります。

あ!\(4{\pi}k_0Q本\)がでてきました!
\(1m^2\)あたりの電気力線の本数=その点の電場の強さという関係がわかっていれば、導出できるよね!

任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例とは?
ガウスの法則
・\(1m^2\)あたりの電気力線の本数=その点の電場の強さ
・任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例し、
$$4{\pi}k_0Q本=\frac{Q}{\varepsilon_0}本$$

2番目の、『任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例』ってなんですか?
まず、『閉曲面』という言葉の解説からです!
閉曲面とは、閉じた部分で囲った面のことを言います。
先ほどの導出で、正電荷を\(1m^2\)で囲ったり、\(4{\pi}r^2\)で囲ったりしたあれのことです。
実は、ガウスの法則では、任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例するのです!

つまり、囲った部分の外にある電荷は、入らないということですか?
その通り!閉曲面の外にある電荷が作る電気力線は、閉曲面の中に入ってきても必ず外に出ていくから、湧き出す電気力線に入らないんだ!

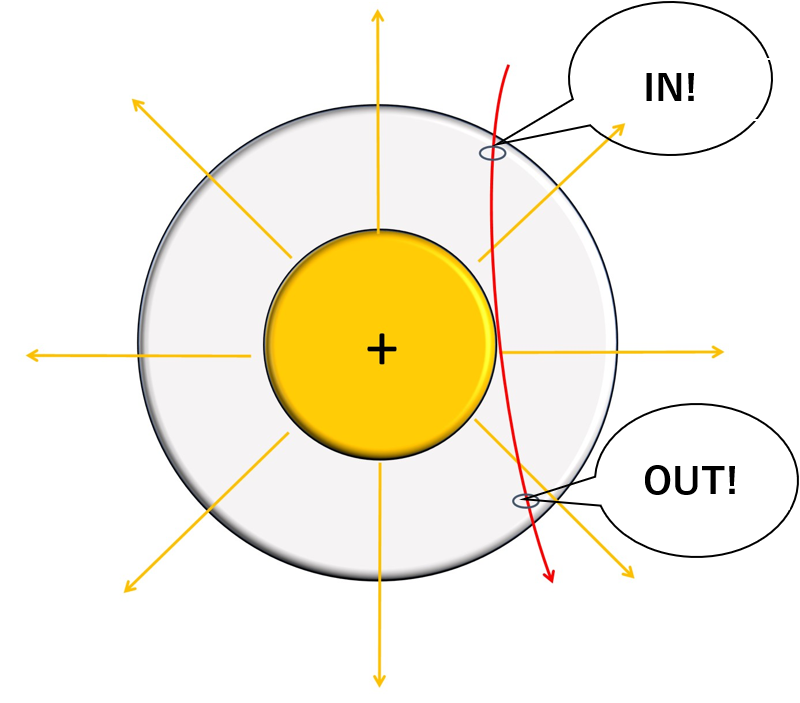

なるほど!つまり、ガウスの法則について考えるときは、閉曲面で囲った内部にある電荷のみを考えればいいのですね!
そうだね!閉曲面の外にある電荷は考えないって覚えておこう!

まとめ
今回は、ガウスの法則についてと、どうして4πkQ本になるのかについて例題を絡めて詳しく説明してきました!
ガウスの法則の言葉の定義と、電気力線が4πkQ本になる導出は非常に大切ですので、しっかりと理解しておきましょう!
ガウスの法則
・\(1m^2\)あたりの電気力線の本数=その点の電場の強さ
・任意の閉曲面から湧き出す電気力線の本数は、閉曲面内の電荷のみに比例し、
$$4{\pi}k_0Q本=\frac{Q}{\varepsilon_0}本$$
今回は以上です。
関連記事電場中で金属内部の電場が0になる理由は?【電場とからめて徹底解説】



