【高校物理】波の式の作り方は3ステップ！正弦波の導出をわかりやすく解説

悩んでる人

・波の式の作り方がわからない
・式がどうやって作られているかわからない
・そもそも波の式って何？

波動の範囲って、イメージがつきにくいせいか、苦手な人が多い分野ですよね。

特に、波の式に関しては、符号がわかりづらくて難しく感じてしまいがちです。

しかし、波の式はたった3ステップで簡単に作ることができてしまうのです！

そこで今回は、参考書よりも詳しく、しかもわかりやすく波の式の作り方について、話していきます。

波の表し方は2種類ある！

そもそも、物理の世界では、波の表し方は2つあります！

まずは、2つのグラフの違いを知らないと、波の式は立てることができませんので、『初めて知った！』という人はしっかり勉強しておきましょう。

そして、今回波の式を立てるに使っていくのは、横軸が\(t\)のグラフである（\(y-t\)）グラフです。

悩んでる人

横軸が\(x\)のグラフ（\(y-x\)）グラフは波の式が立てられないのですか？

（\(y-x\)）グラフは、自分で（\(y-t\)）グラフに書き換える必要があるから、その方法も教えるね！

塾長

それでは、さっそく波の式を立てていきましょう！

【マネでOK！】波の式の作り方は3ステップで完了

冒頭でも話した通り、波の式は3ステップで作ることができます。

それでは、実際に例題を見ていきましょう。

例題

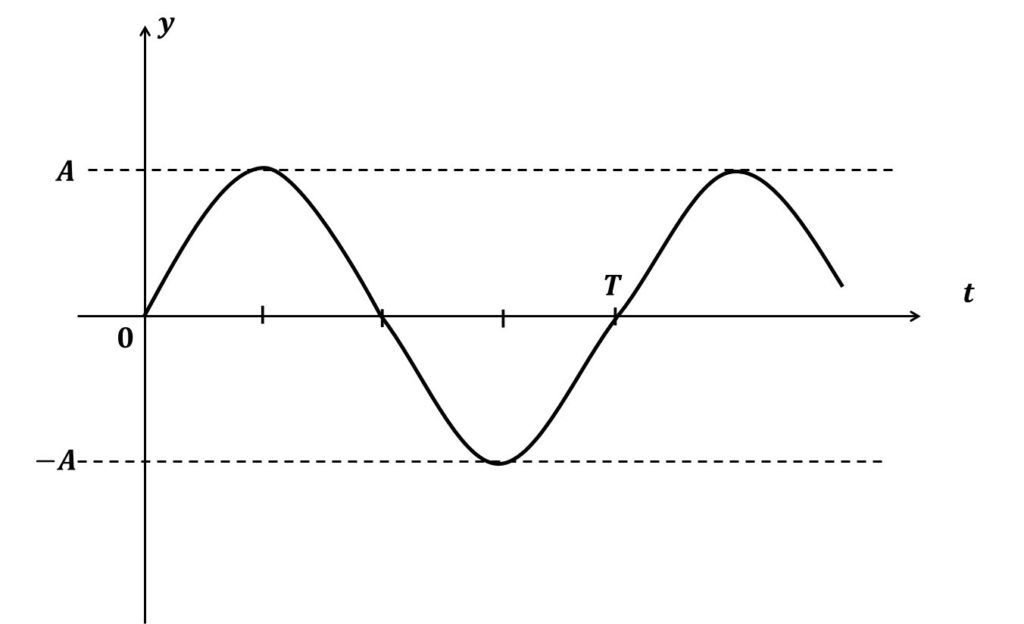
\(x=0\)における媒質の単振動が上のように与えられたときの、時刻\(t\)における変位\(y\)を表す式を波長\(\lambda\)、周期\(T\)を用いて表せ。ただし、波は\(x\)軸正方向に\(v\)で進行するものとする。

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

➀（\(y-x\)）グラフは（\(y-t\)）グラフに書き換える！

今回、グラフを見てみると、最初から（\(y-t\)）グラフになっているので、このステップは飛ばして大丈夫です！

➁ある1点の単振動を時間の関数で表す

今回の波は、\(x=0\)における媒質の単振動の様子が書かれています。

波の形は、振幅がAのsin関数なので、グラフから\(x=0\)における時刻\(t\)の波の変位は

$$y(0,t)=Asin\omega t・・・➀$$

と書くことができます。

\(y(0,t)\)というのは、\(x=0\)という場所に、時刻\(t\)に発生する波の高さ\(y\)という意味だよ！

塾長

➂➁が位置\(x\)に届くのにどれくらいかかるか考える

さて、いよいよ最後のステップです。

最後は、➁が位置\(x\)に届くのにどれくらいかかるか考えていきます。

ここからがとても大切なので、しっかり理解してくださいね！！

\(x=0\)で発生した波と同じ高さの波が、\(x=x\)に来るまでにかかる時間は、道のり÷速さで

$$\frac{x-0}{v}=\frac{x}{v}$$

となります。

座標の距離を出すには、2点の座標の（大ー小）をすればいいから、道のりは\(x-0\)になるよ！そして、この下がめちゃくちゃ大事！！

塾長

つまり、位置\(x\)に、時刻\(t\)に届く波の高さは、\(x=0\)において、時刻\(t-\frac{x}{v}\)に発生した、波と高さが等しくなります！

悩んでる人

混乱しました。

上の図のように、位置\(x\)に来た人は、当然、家（\(x=0\)）を到達した時刻\(t\)よりも\(\frac{x}{v}\)だけ早く出た人と、同一人物ですよね？

同じように考えれば、位置\(x\)に、時刻\(t\)に届く波の高さは、\(x=0\)において、時刻\(t-\frac{x}{v}\)に発生した、波と高さが等しくなる、といえます！

そして、言葉の通りに式にすると、

$$y(x,t)=y(0,t-\frac{x}{v})・・・➁$$
(位置\(x\)に、時刻\(t\)に届く波の高さ)
=(\(x=0\)において時刻\(t-\frac{x}{v}\)に発生した波と高さ)

となります。

➀の式と➁の式を見比べて、

$$y(0,t)=Asin\omega t・・・➀$$$$y(0,t-\frac{x}{v})=Asin\omega (t-\frac{x}{v})$$$$=Asin2\pi (\frac{t}{T}-\frac{x}{\lambda})・・・答え$$

となります。

最後の式変形では、\(\omega=\frac{2\pi}{T}\)を代入しているよ！

塾長

まとめ：持っている問題集を使って波の式を作ってみよう！

今回は、波の式の作り方について話してきました。

波の式は、以下の3ステップで作ることができましたね。

今回の内容は、非常に大切なので、何度も読み込んでおきましょう！

このページが理解できた人は、

について話していくので、次の記事もご覧ください！

関連記事【負の方向に進む波の式の作り方は？たった3ステップで完結します】