今回は、下の例題を使って『軌跡図』を使った解き方について解説していくよ!

※この記事は、前回の記事とリンクしていますので、まだの人は【単振動を完全攻略!!どこよりもわかりやすく例題とともに単振動問題を解説!】をご覧ください。
例題
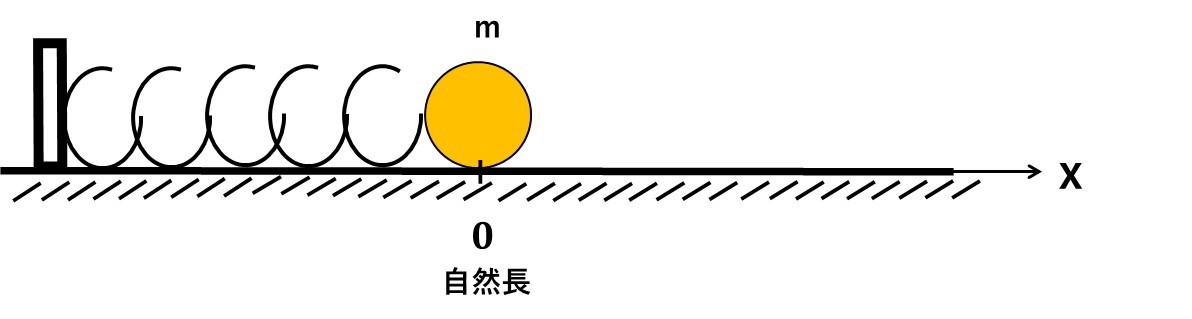
なめらかな水平面において、ばね定数kのばねを壁に固定し、他端に質量mの球をつなぐ。自然長を原点として、図のようにx軸をとり、時刻t=においてx=Aから球を静かに放すと、球は単振動し始めた。
(1)位置xを時間tの関数として、表せ。また\(x=-\frac{A}{2}\)を初めて通る時刻を求めよ。
※いつも通り、まずは自分で考えてみましょう!自分で解くことで、『解くうえで何が足りないのか』が明確になります!
問題の解答
例題

なめらかな水平面において、ばね定数kのばねを壁に固定し、他端に質量mの球をつなぐ。自然長を原点として、図のようにx軸をとり、時刻t=においてx=Aから球を静かに放すと、球は単振動し始めた。
(1)位置xを時間tの関数として、表せ。また\(x=-\frac{A}{2}\)を初めて通る時刻を求めよ。
まずは、位置xを時間tの関数として表していきます。

そんな公式ありましたっけ?
ここで、『軌跡図』を使っていくんだよ!

軌跡図を使って解く

単振動は、等速円運動をとこから見た運動だったので、紙面下向きにt、右方向にx軸を取ると、上のような軌跡を描きながら運動していることがわかります。
では、赤色の曲線はどんな関数かな?


あ!振幅がAのcos波です!
これをもとに、位置xの式を立てると、
$$x(t)=Acoswt$$
となります!前回の(1)で\(w=\sqrt\frac{k}{m}\)だったので、これを代入して
$$x(t)=Acos\sqrt\frac{k}{m}t・・・答え$$
となります。
また、上の式を使って、\(x=-\frac{A}{2}となる時刻t_1\)は、
$$-\frac{A}{2}=Acos\sqrt\frac{k}{m}t_1$$
$$\sqrt\frac{k}{m}t_1=\frac{2}{3}t$$
$$\thereefore t_1=\frac{2\pi}{3}\sqrt\frac{m}{k}・・・答え$$
となります。このように、単振動の位置を求めるときは『軌跡図』を使って求めることができます!
ポイント
単振動の位置は、『軌跡図』を使って求める!
【補足】もし\(x=-\frac{A}{2}\)での速度を聞かれたら?
今回は、位置xを求める問題でしたが、速度を求めろと言われたときは、位置の式を微分しましょう!

$$x(t)=Acos\sqrt\frac{k}{m}t$$
もし、速度を聞かれたら、
$$v=\dot{x}$$$$=-A\sqrt\frac{k}{m}sin\sqrt\frac{k}{m}t$$
となります。
\(x\)の上についている・は『微分』という意味だよ!そして、この計算は数Ⅲの範囲だけど、こうやって求めることもできることは覚えておこう!

まとめ:軌跡図を使って単振動を攻略しよう!

今回は、参考書にあまり書かれていない『軌跡図』について話してきました。
物理のエッセンスにも少しだけ描いてあるのですが、大きくは書いてなく、中には知らなかった人もいるのではないでしょうか。
今回の解き方は、数学の知識を使うやり方でしたが、数学の基本が身についている人にとっては、そんなに難しくはないはずです。
あまりできなかった人は、数Ⅱの三角関数を復習してみてください。

