運動方程式をあなたは本当に理解できてる？？運動方程式を理解して力学の点数を爆上げする

悩んでる人

運動方程式の本当の意味とか言われると、何か不安なんですけど、、

確かにいきなり言われるとびっくりするよね（笑）けれど、力学で点数を取るためには大事なことなんだ！

塾長

そこで今回は、力学で点数を爆上げするために、力学の根幹でもある運動方程式の理解を深めていきます！

この記事を読めば、『運動方程式の使い方がイマイチわからない』『式の立て方がわからない』といった悩みは解決されますよ！

まだ、前回の記事を読んでない人は、以下の記事を参考にしてみてください。

関連記事ばねの弾性力の大きさと向きは？ばね合成の例題とともにわかりやすく説明

まずは運動方程式の基本公式を確認する！

まず、運動方程式について確認しましょう！

運動方程式は、

$$\LARGE m\vec{a}=\vec{F}$$

でした！

それぞれの文字についても、確認しておきましょう！

太字の部分は特に大切ですので、しっかり覚えておいてください！

運動方程式の意味とは

日本語で説明すると、『質量\(m\)の物体に、力\(\vec{F}\)が働くと、物体には加速度\(\vec{a}\)が生じる』と説明できます。

つまり、力\(\vec{F}\)が原因で、加速度\(\vec{a}\)が生じるという結果になるのです！

悩んでる人

力が原因で加速度が生まれるのは、分かったのですが、その前に文字の上についている矢印が気になるのですが、、

その矢印は、ベクトルだよ！世の中には、大きさのみ持つ『スカラー』と、大きさと向きを持つ『ベクトル』があるんだ！

塾長

スカラー・・・大きさのみを持つ　 （例）質量、長さ、速さ

ベクトル・・・大きさと向きを持つ　（例）速度、力積、電場

悩んでる人

わわわ、、ベクトルとかいきなり、わけがわからなくなりました、、

ベクトルが苦手な受験生は結構多いんだ。そんな時、ベクトルをスカラーに変える方法があるんだよ！

塾長

悩んでる人

いったいどんな方法ですか？！

それは、加速度の方向を正方向として、軸を取ってしまう方法だよ！

塾長

塾長

それでは、例題で確認していきましょう！

例題：運動方程式の解き方

例題

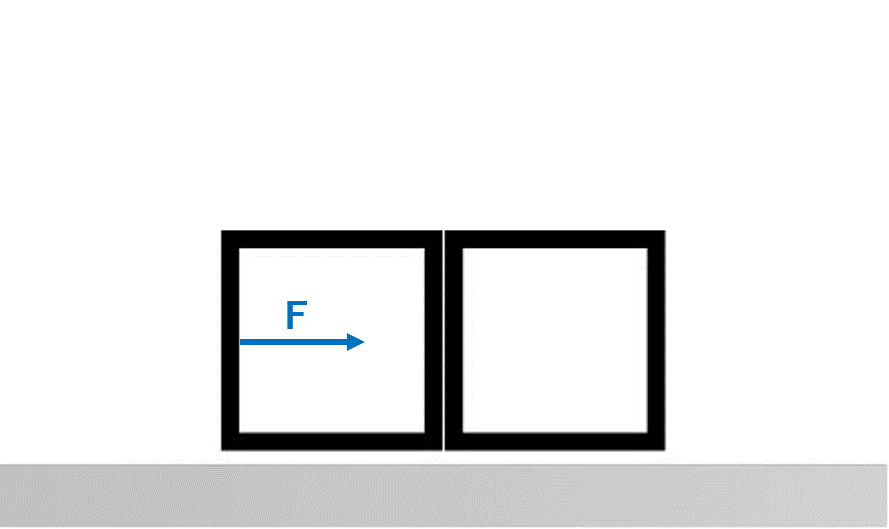
2つの物体を接触させた状態で、滑らかな床の上に置いた。左側にある物体Aの質量をm、右側にある物体Bの質量をMとする。左側にある物体Aの左側から、図の向きにFの大きさで押すとき、全体の加速度の大きさはいくつになるか。また、AがBに及ぼす力の大きさはいくらになるか答えよ。

※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！

それでは、解説していくよ！まずは、以下の手順に従って力を描いていくよ！

塾長

1.力を描き込む！

力を描くときに気をつけるポイントは、以下の3つでしたね！

今回は、図がごちゃごちゃするのを防ぐために、重力と垂直抗力は描かないので、気にしないでください。

さて、上の手順に従って図を描くと、

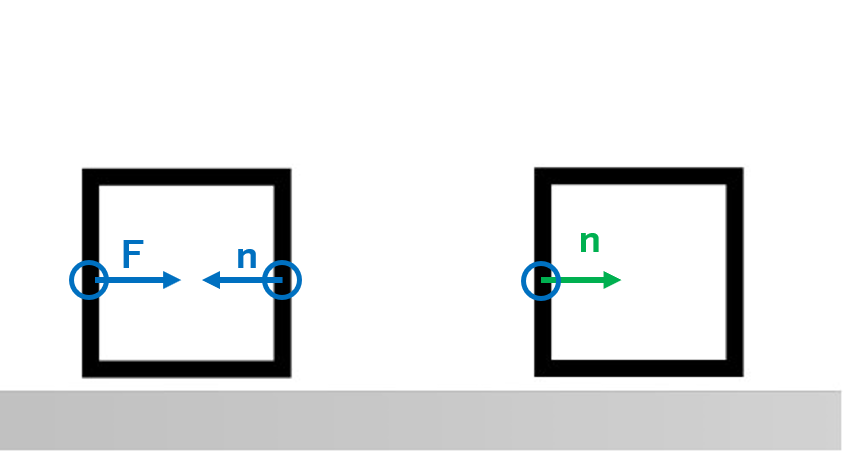
となります。

緑の矢印は、作用・反作用の法則ですね！

よく覚えていたね！それじゃ、運動方程式を立てていくよ！

塾長

2.運動方程式を立てる！

まずは、加速度方向に軸を立てますが、今回は右向きに動くので、右方向を正方向としましょう！

塾長

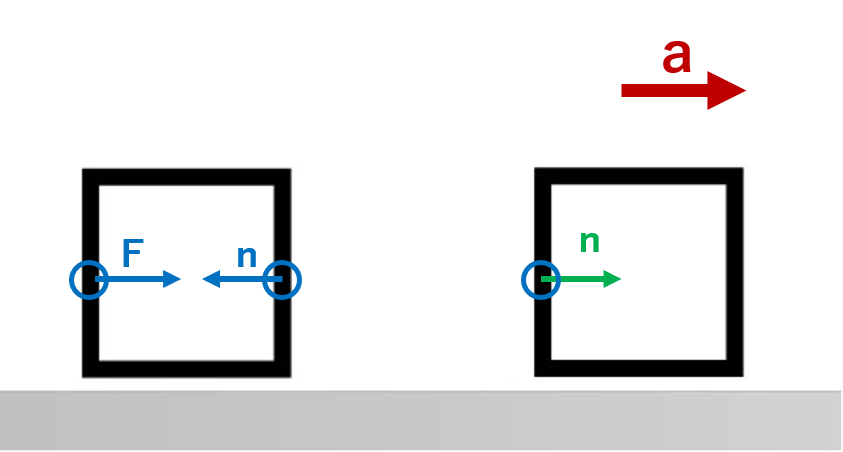
それでは、運動方程式を立てていきます！

物体Aについて

物体Aの質量はmで、Fは軸と同じ方向に、nは軸とは反対方向に力を受けているので、

$$ma=F-n・・・➀$$

と書くことができます！

物体Bについて

物体Bの質量はMで、nは軸と同じ方向に力を受けているので、

$$Ma=n・・・➁$$

と書くことができます！

$$ma=F-n・・・➀$$$$Ma=n・・・➁$$

➀➁を連立して、aとnの値を求めると、

$$a=\frac{F}{M+m}$$$$n=\frac{MF}{M+m}$$

となります。

このように、運動方程式は加速度方向に軸を取って、着目物体一つひとつについて考えていけば、難しくはないんだ！

塾長

まとめ：

そこで今回は、力学で点数を爆上げするために、力学の根幹でもある運動方程式の理解を深めてきました！

まとめると、以下のようになります。

これらのことを、しっかりと覚えておきましょう！

次は、この内容をもとに、『もし糸に質量があったら』ということを考えていきます。

今回は以上です。

関連記事【6割以上が騙される】軽い糸の物理問題に隠された秘密とは！？